第九次习题课

内容：第十二章第七节至第十一节。

重点：求二阶微分方程的解

难点：二阶非齐次线性方程的解

专题：微分方程解题思路总结

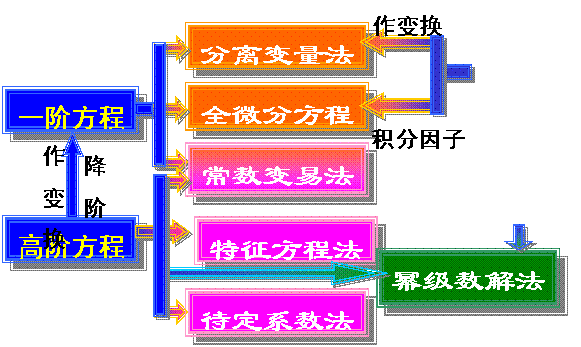
微分方程的解法特点：

1.积分，相同变量及其微分分离开来积分。

2.对于特解，可以通过猜测加验证。

3.对齐次转非齐次，或简单到复杂，可以先求简单的，然后常数变易。

4.变量代换：利用中间变量，分离变量或降阶等，将方程化为易求的形式。

5．将实数上的微分方程在复数上讨论，然后再将解转回实数。

专题：高阶微分方程求解问题

一、 二阶（高阶）常系数微分方程解的结构

标准形式：

齐次：双根：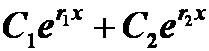

单根：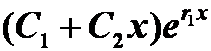

复根：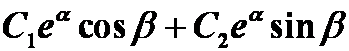

非齐次：将幂函数、指数函数与三角函数的组合可以通通归结到一种形式：

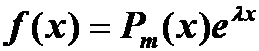
注：这里可为实数，也可为复数！当然，觉得这种方法难理解就直接套公式！

特解形式：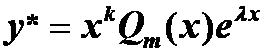

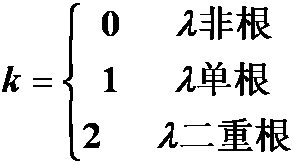
二、 求解方法

1. 降阶法（前面介绍）；

2. 特征方程法；

3. 待定系数法；

3.常数变易法（少用）

例1 已知

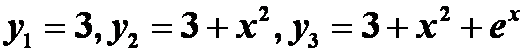
都是微分方程

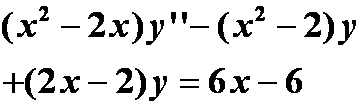
的解。求此微分方程的通解。

答案：。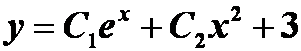

例2 验证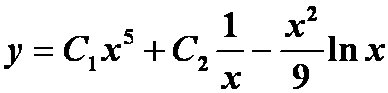

是方程的通解。

提示:解的验证易。通解需要验证与线性无关。

例3 验证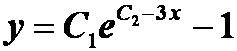是方程

的解。但是它不是通解。

提示：是解的验证易。另外y可以写成

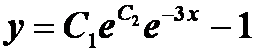
等效于，因此实际上它只有一个常数，因此不是通解。

例4 求的通解

提示：降阶法

答案：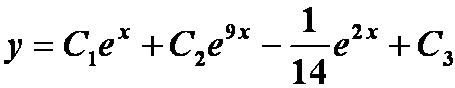

例5求下列5阶常系数线性微分的通解

提示：特征方程法

答案：

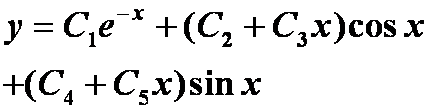
例6 解下列两个方程

（1）

（2）

提示：待定系数法。但是两个小题有不同的解法，第一小题适合构造虚方程，第二个小题适合待定系数套公式。

答案：（1）

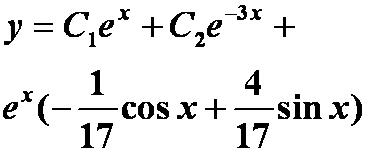
（2）

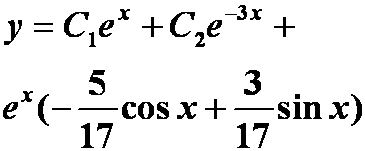
例7 解方程

答案：

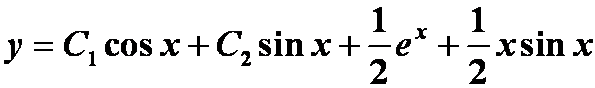
补充例题：