第八次习题课
内容:第十二章第一节至第五节。
重点:微分方程的概念、线性微分方程的求法。
难点: 积分因子与凑微分求微分方程
专题:一阶微分方程的求法判断次序:
第一步:先判断x,y的次数,若有一个不超过一次,则作为线性微分方程来解。若有一个为1次和n次,判断是否伯努里方程。
第二步:判断是否齐次,若是,则换元u=y/x(或u=x/y).
第三步:判断是否可分离变量。(对于齐次方程不好求的话也可以考虑)
第四步:判断是否全微分方程。
第五步:考虑乘积分因子(少见)。
注:往往微分方程不止一种解法。
例1(书269页1(7))求下列微分方程的通解:
![]()
分析:此题很容易想到全微分,实际上它可分离变量。
答案: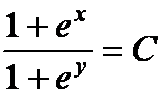
例2. 分别解下列微分方程
(1)
![]()
提示:先化一阶线性微分方程标准形式;
答案: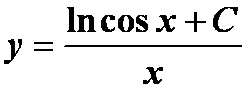
(2) 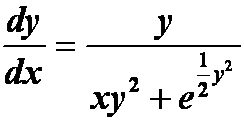
提示:将x作为函数,y作为自变量,变一阶线性。
答案: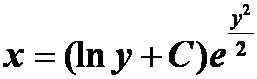
例3 求下列方程的通解。
(1)
![]() 提示:齐次方程,令u=y/x.
提示:齐次方程,令u=y/x.
答案: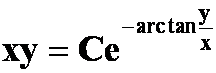
(2)![]()
提示:平移后可得齐次方程,再类似(1)的方法。
平移:令![]()
答案: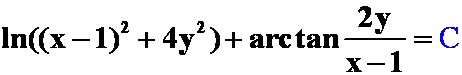
例4
求下列方程组的通解
![]() 的通解。(第三次作业第7题)
的通解。(第三次作业第7题)
提示:是全微分方程。全微分法小结:
方法1:曲线积分法(无技巧,注意代值)。
方法2:凑微分1:分项组合(技巧强);
方法3:凑微分2:不定积分(无技巧)。
分项组合原则:1)同一类变量一定可分;2)微分内外有相同结构可代换的可分;3)udv+vdu形式的可分。
(答案:分项组合
![]()
解得: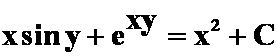 )
)
例5. 用组合法求下列微分方程的通解:
(1)![]()
提示:组合积分因子。
答案: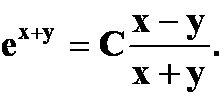
(2)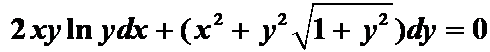
分析:此题有一定难度,用全微分法做。直接全微分不可。分项再观察。
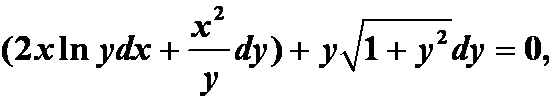
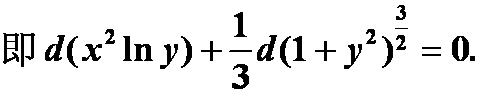
答案: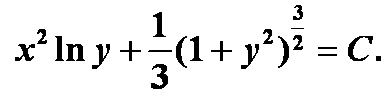
专题:微分方程的变量替换总结
变量替换的目的:第一.简化;第二.化成易计算的标准形式;第三.整合,将数个变量整合成一个变量。
常见的有:
1.
u=xy;
特点:du/dx=y+xdy/dx
用途:三角等函数内有乘积常用于替换后分离变量。
2.
u=y/x或u=x/y;
特点:dy/dx=u+xdu/dx;
用途:常用于解齐次微分方程。
3.
u=ax+by;
特点:du/dx=a+bdy/dx
4.![]() ;
;
用途:用于伯努里方程。
例6. 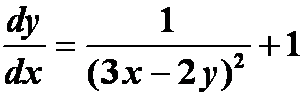
提示:令![]()
答案:
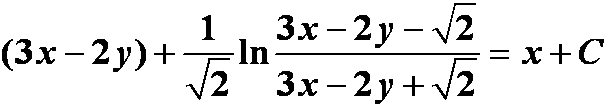
例7 (书282页9(3))
![]()
分析:一般来说有一个原则:三角函数,对数函数内有xy或y/x等,优先将之代换。
令u=xy;代换得
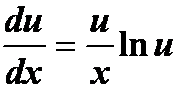
答案:![]() 或
或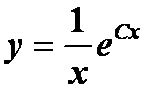
例8 ![]()
提示:齐次方程,令u=x/y.
答案:![]() .
.
专题:微分方程应用题
此部分不是重点,主要要求大家能对几何方面的应用能够会列微分方程。无需做太难的题。
微分方程与以前学的方程无本质的区别。只是以前学的方程为F(x,y)=0形式,现在是![]() 或
或![]() 等形式,变量之间的关系不变!
等形式,变量之间的关系不变!
列方程的关键是找到一个等式,等式中含自变量、因变量以及它们的微分即可。
例9 在xoy面的第一象限有一条曲线,过曲线上任一点垂直于x轴的直线与两坐标轴以及此曲线所围成的曲边梯形的面积之值等于该段曲线长度的两倍,曲线通过(3,2),求曲线的方程。
提示:
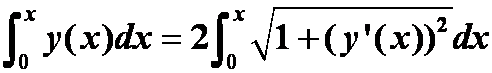
答案: 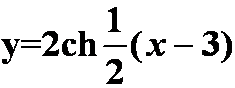 .
.
补充习题:
第一次作业第4题:
设非负连续函数![]() 满足关系式
满足关系式
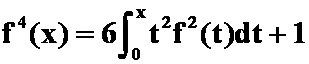 ,则
,则![]() ()。
()。
A.![]() ; B.
; B.![]() ;
;
C.![]() ; D.
; D.![]() 。
。
解 选(A),方程两边求导,得![]() ,两边积分得
,两边积分得![]() ,又
,又![]() ,得
,得![]() 。
。
第四次作业第3题:
下面结论中不正确的是( )。
A.方程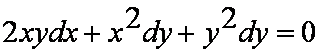 是全微分方程。
是全微分方程。
B.方程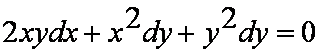 可化成齐次方程。
可化成齐次方程。
C.积分方程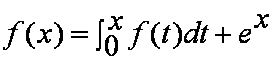 的解与微分方程
的解与微分方程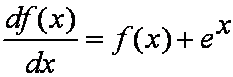 的解相同。
的解相同。
D.积分方程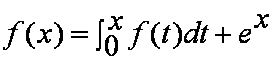 的解与定解问题
的解与定解问题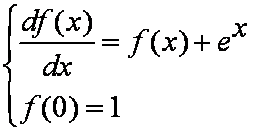 的解相同。
的解相同。
解 选(C)。
第四次作业第6题:
求方程
![]()
![]() 的通解。
的通解。
解 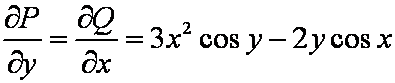 ,这是全微分方程。用分项组合凑微分的方法,可得
,这是全微分方程。用分项组合凑微分的方法,可得
![]()
![]() ,
,
故通解是![]() 。
。