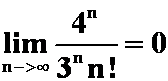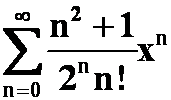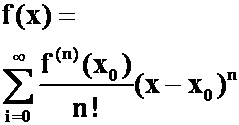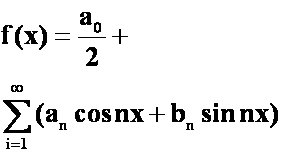第七次习题课
内容:第十一章第四节至第八节。
重点:函数的幂级数展开与傅里叶展开
难点:傅里叶级数。
专题:函数的幂级数展开方法总结。
一、 直接法。(等比、裂项或递推)
二、 换元法。
三、 四则运算法。
四、 逐项求导(积分)法。
例1已知函数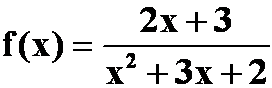 ,
,
(1)
将函数展开成x的幂级数;
(2)
将函数展开成(x+4)的幂级数。
提示:裂项加等比。注意针对不同的展开点有不同的展开方法。
(答案(1)
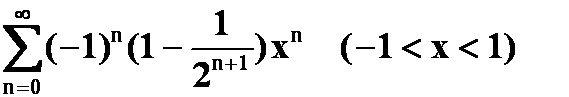 (2)
(2)
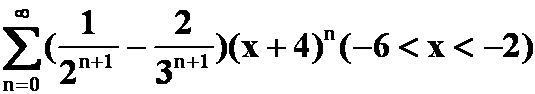
例2 将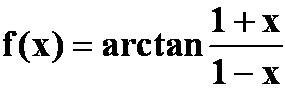 展开为x的幂级数。
展开为x的幂级数。
提示:求导后展开,再逐项积分。先导后积。(注意积分后的下限!)
答案: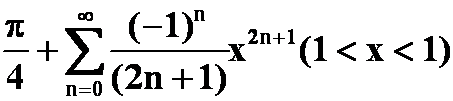
例3 将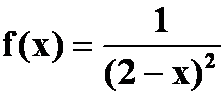 展开成x的幂级数。
展开成x的幂级数。
提示: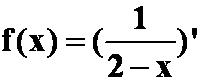 ,对导数里面的函数展开,再逐项求导。先积后导.(注意首项)
,对导数里面的函数展开,再逐项求导。先积后导.(注意首项)
答案: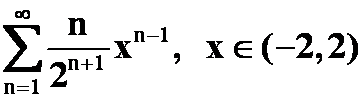
例4 将函数![]() 展开成x的幂级数。
展开成x的幂级数。
提示:四则运算+换元.
答案:

例5 展开
提示:换元+四则运算+先导后积。
答案: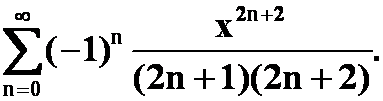
专题:求级数的和(或幂级数的和函数)
一.常见数项求和法。
1.等比; 2.错项相减。
二.逐项求导与逐项积分。(上一次习题课讲过,本次习题不举例)
三.利用泰勒级数(换元或加减项等)。
四.利用傅里叶级数(少见)。
例6 求下列级数的和。
(1)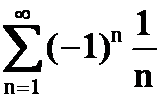
提示:利用![]() 的泰勒展开式。
的泰勒展开式。
答案:![]() .
.
(2)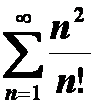
提示:利用![]() 的泰勒展开式,再求导两次…
的泰勒展开式,再求导两次…
答案:2e.
例7:求下列幂级数的和函数
提示:利用指数函数的泰勒展开式。关键在于如何搭配通项。要经历几个步骤。
(答案: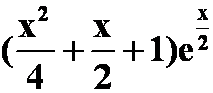 )
)
(2)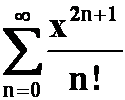 并求:
并求: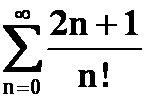
提示:利用指数函数的泰勒展开式。
(答案:![]() ;
;![]() )
)
专题:函数的傅里叶展开。
两种展开法的比较:
|
|
幂级数展开 |
傅里叶展开 |
|
公式 |
|
|
|
条件 |
f(x)在 |
周期函数f(x)在一个周期内最多有限个第一类间断点和极值点。 |
|
范围 |
一般初等函数均可。 |
周期函数或定义域为有限区间的函数。 |
|
局限 |
条件较强(比后者强)。 |
应用范围小。间断点不收敛于函数值。 |
|
应用 |
近似计算。计算特殊积分。 |
波与振动问题。 |
注意:函数的傅里叶展开,我们只需要针对简单的函数能套公式些出展开式即可,比必要做太多其它题型。
例8 设下列函数的周期为![]() ,求其傅里叶级数。
,求其傅里叶级数。
![]()
提示:偶函数。
答案: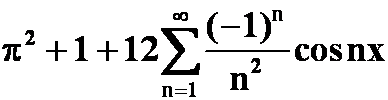
(![]() )(注意级数做了延拓)
)(注意级数做了延拓)
例9 设周期函数在一个周期内的表达式为
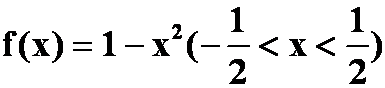
试将其展开成傅里叶级数。
提示:偶函数,![]()
答案: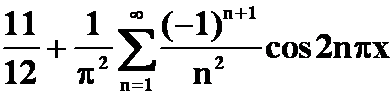
(![]() )
)
补充习题:
第六次作业第4题:
4.函数 关于
关于![]() 的幂级数展开式为( )。
的幂级数展开式为( )。
A.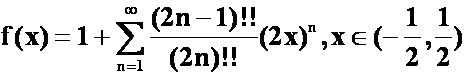 ; B.
; B.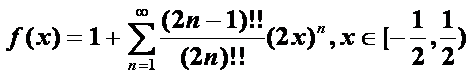 ;
;
C.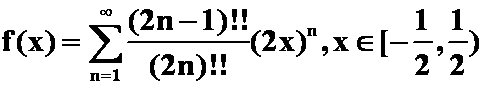 ; D.
; D.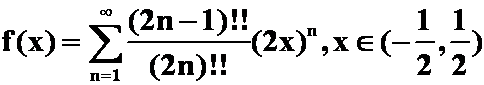 。
。
解 选B.
第七次作业第7题:
7.将函数![]() 展开成
展开成![]() 的幂级数。
的幂级数。
解  而
而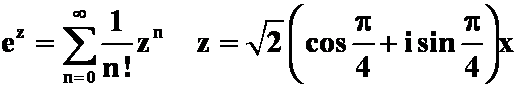
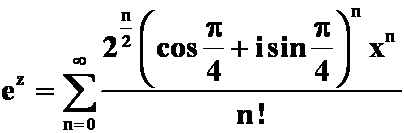
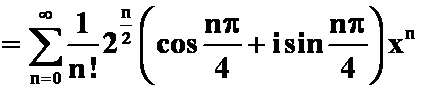
![]()
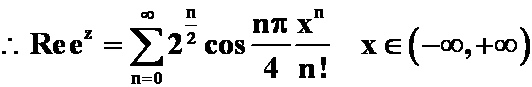
即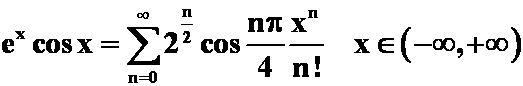
第九次作业第7题:
7.将函数![]() 展开成
展开成![]() 的幂级数,并据此证明
的幂级数,并据此证明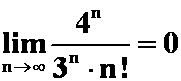 .
.
解 因为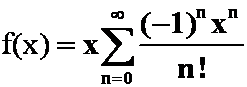 ,
,
所以 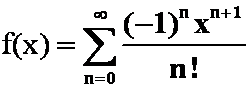
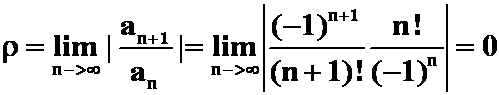
所以 R=+∞,收敛区间为(-∞,+∞)
又 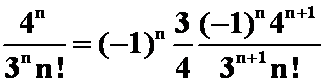
由上知 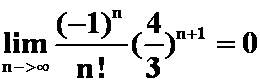
所以