第六次习题课
内容：第十一章第一节至第三节。
重点：常数项与幂级数的审敛法。
难点：比较审敛法以及其极限形式。
专题：常数项级数的审敛法总结比较。
|
一般项级数 |
正项级数 |
交错级数 |
|
1．若 2. 若 3.按照基本性质。 |
||
|
4.绝对收敛
|
4.充要条件 5.比较法 （及极限形式） 6.比值法 7.根值法 |
4. 绝对收敛 5. 莱布尼兹 (条件收敛)
|
1、 比较审敛法
优点：“放缩”灵活。缺点：要找一个级数作参照。
2、 比值审敛法
优点：方法简单，无需参照。优先选此法。
缺点：比值为1的情形无法判别。
3、 根值审敛法
优点：系数幂次较高，不易用比值时可用它。
缺点：根的极限常不易求，也存在比值为1无法判别。
审敛原则：
一般项往正项靠，
放缩同阶无穷小。
常用等比p级数，
极限性质离不了。
常见的错误：
（1） 将级数收敛的必要条件当成充分条件。
（2） 将比较审敛法用于非正项级数。
（3） 比较审敛法的极限形式与比值审敛法混淆
例1. 判断下列常数项级数是否收敛
（1）
一般项往正项靠，绝对收敛
答案：收敛。
（2）
常用等比p级数，比较
答案：收敛
（3）
常用等比p级数，
提示：遇到阶乘一般用比值(类似等比)。
答案：发散。
（4）
放缩同阶无穷小。比较
答案：收敛。
（5）
极限性质离不了。
提示：用比较极限形式。易与比值混淆。注意比值是用自己的项比，比较的极限形式是与其它级数比。往往比较的极限形式是利用等价或同阶无穷小。俩级数的大小关系不是特别明朗时用。
答案:收敛。
例2 判别下列级数的敛散性
（1）
提示：比较+比值。
答案：收敛。
（2）
提示：比较法的极限形式
答案：发散。
（3）
提示：根值审敛法
答案：发散。
例3 判别下列级数是否收敛，若收敛，是绝对收敛还是条件收敛？
（1）
提示：遇到交错级数，一般是先打绝对值判断它是否绝对收敛，若绝对收敛，自然原级数收敛！若非绝对收敛，则用莱布尼茨判别法判断条件收敛（条件收敛不是说收敛需要条件，它本身是收敛的！）。
（答案：条件收敛）
(2) 
（答案：绝对收敛）
(3)(书207页) 
提示:比较前后项大小时可以用比值!
答案:发散.
专题：用数项级数与函数项级数的关系及解题。
关系：函数项级数当未知量取定值时即数项级数。
解题：1.函数项级数求收敛区间可以用数项级数的比值审敛法做。
2. 求数项级数的和时，先求对应函数项级数的和（可用逐项求导与逐项积分），然后代入特殊值。
例2 求幂级数的收敛区间
（1）
答案： 
（注意边界需要另外考虑）
（2） 
（注意没有奇数项!）
答案：
例3求下列级数的和
（1）
（2）
（3）
提示：通过幂级数求数项级数的和。必须注意：1.级数通项加
的某次幂，幂次须为了逐项求导或积分方便；2.通项中分子复杂的常先积分，分母复杂的常先求导。
答案：（1）8.
（提示：用
，x=1或
，x=
）
（2）5 （提示：用
，x=1）
（3）2ln2-1
（提示：用
，x=1）
例4 求下列幂级数的和函数
（1）
（2）
提示：（1）先逐项求导；（2）先逐项积分。(注意首项)
答案：（1）
（
）
（2）
（
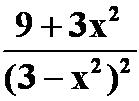补充：
第1次作业第3 题
设级数
收敛，而
发散，则级数
和
分别是（C）。
A．收敛的； B．发散的 ； C．发散的和可收敛可发散的； D.可收敛可发散的和发散的
第3次作业第1题
若条件收敛，绝对收敛，则级数是 。
解 收敛是显然的。假设是绝对收敛，则由
可知绝对收敛，与已知矛盾。所以级数条件收敛
第三次作业第4题
下列结论正确的是（C）。
A．
若收敛，则
收敛；B．若发散，则发散；C．若收敛，则
收敛； D．若收敛，则收敛。
解 对A，B，D，可举出反例。对C，因为
，根据课本第205页定理10可知。