第五次习题课
内容:第十章第四节至第七节
重点:两种类型的曲面积分、高斯公式
难点:高斯公式、斯托克斯公式
专题:两类曲面积分与重积分的关系
![]()

说明:(1)一代,二换,三投:代z,换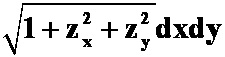 ,D为
,D为![]() 的投影。
的投影。
一代,二投,三定向:代z,D为![]() 的投影,定向:确定曲面的侧的方向。
的投影,定向:确定曲面的侧的方向。
(2)求曲面积分的重点就是这个“投”字!投影要以计算(第七章讲过!)为主,作图为辅。难也难在于投影有时候不是投在xoy面,而是投在xoz面和yoz面。
例1计算曲面积分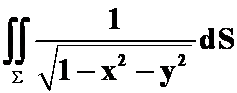 ,其中
,其中![]() 为锥面
为锥面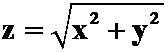 被柱面
被柱面![]() 所截下的有限部分.(第五次作业第五题)
所截下的有限部分.(第五次作业第五题)
分析:首先确定是哪一类积分,然后“以直代曲”,这里有两个面,前者是确定被积曲面的;后者是用来确定化重积分的积分区域的。
答案:![]()
例2 计算曲面积分
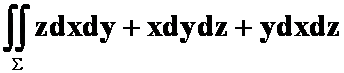
![]() 是柱面
是柱面![]() 被平面
被平面![]() 所截得的在第一卦限的前侧。
所截得的在第一卦限的前侧。
问:用高斯公式方便吗?
分析:注意投影及其符号。
答案:![]()
专题:各种积分之间的关系
1图示:
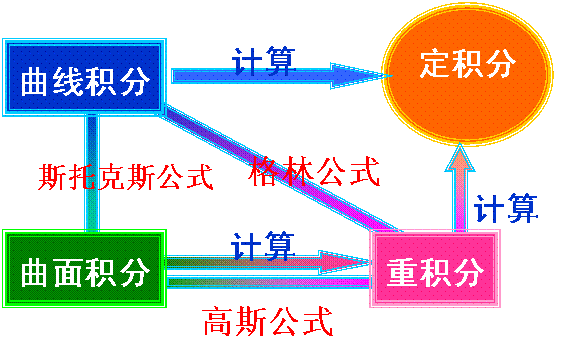
2.现在为止,已经介绍了所有各种定积分与重积分的变式。综合起来,可以用下列口诀记忆:
以直代曲微转换
变量统一看相关
积分升级看闭域
偏导只作导数观
3.所有积分的规律总结:
所有积分,有两大要素:一是被积函数部分;二是被积微分部分。其中微分部分又含微分形式和范围。形形色色的积分均从第二个要素变化而来,比如:
对定积分的微分部分变化,将微分范围由x轴的一段变成曲线的一段,就成了曲线积分,微分形式不变的是第一类,微分形式改弧长的是第二类。定积分可作为两类曲线积分的特殊情形。
对二重积分的微分部分变化,将微分范围由xoy面的区域变成曲面的一块,就成了曲面积分,微分形式不变的是第一类,微分形式改面积的是第二类。二重积分可作为两类曲面积分的特殊情形。
综上:积分变量分成1维、2维、3维;1维对曲线(直线);2维对曲面(平面);三维对立体。总的说来,对积分变量的处理仍然是“以直代曲”:以对直线的定积分求曲线积分;以对平面的二重积分求曲面积分!
例3求曲面积分
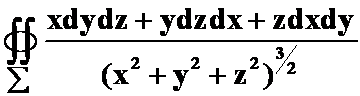 ,其中
,其中![]() 为球面
为球面![]() 的外侧.(据第六次作业第七题略改)
的外侧.(据第六次作业第七题略改)
提示:复杂的形式的积分,第一:是否据![]() 可将变量代常量;第二:能否用对称性;第三:能否根据两类积分的关系转化,一般都是第二类化第一类,此种情况一般被积函数含有
可将变量代常量;第二:能否用对称性;第三:能否根据两类积分的关系转化,一般都是第二类化第一类,此种情况一般被积函数含有![]() 的表达式第四:利用高斯公式。此题恰好四种方法都可以用!
的表达式第四:利用高斯公式。此题恰好四种方法都可以用!
答案: ![]()
例4计算
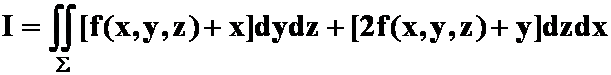
![]() 。其中f(x,y,z)连续,
。其中f(x,y,z)连续,![]() 为平面
为平面![]() 在第一卦限的上侧。
在第一卦限的上侧。
(利用两类曲面积分关系公式,答案:1/2)
例5(第7次作业第6题)计算曲面积分
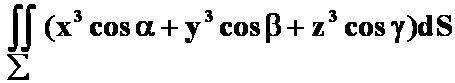 ,其中
,其中![]() 是锥面
是锥面![]() ,而
,而![]() 是锥面
是锥面![]() 上的点
上的点![]() 处外法线的方向余弦.
处外法线的方向余弦.
提示:利用高斯公式,注意加盖封闭。
答案: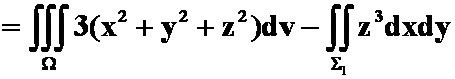
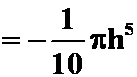
(![]() 为
为![]() 上侧,
上侧,![]() 与
与![]() 所围区域为
所围区域为![]() ,)
,)
例6 计算
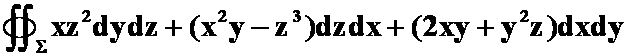 其中
其中![]() 为上半球体
为上半球体
![]()
表面的外侧。
分析:典型的利用高斯公式,记住:只要涉及dxdy,dxdz,dydz在一起的都要想到高斯公式!它是封闭曲面。
答案: 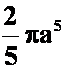 。
。
专题 通量、散度;环流量,旋度的理解及其关系:
通量:通过曲面的场的流量。如:水流的快慢…
散度:一个点产生的场的强度。如电场某点有电荷…
环流量:场在一个封闭环的流量。
旋度:场在某点的旋转的强度。如江水的漩涡…
关系:
1.
不可压缩的流量场(如:水流、电场)流经一个封闭空间的通量(流量)等于封闭空间各处产生的源头强度之和。
2.
流量场流经一个封闭环的环流量相当于环内曲面各点旋转强度之和。
例6求下列向量
![]()
穿过以(3,-1,2)为球心,3为半径的球面![]() 的流向外侧的流量。
的流向外侧的流量。
提示:求通量,封闭曲面积分,用高斯公式;
答案:108![]() .
.
例7求向量场![]() 沿
沿![]() (从z轴正向看去,逆时针方向)的环流量。
(从z轴正向看去,逆时针方向)的环流量。
提示:曲线积分;答案:2![]() 。
。
补充:
第6次作业第3题:
1.设![]() 为柱面
为柱面![]() 被平面
被平面![]() 及
及![]() 所截得的在第一卦限的部分,取外侧;
所截得的在第一卦限的部分,取外侧;![]() 在
在![]() 面、
面、![]() 面与
面与![]() 面上的投影区域分别记为
面上的投影区域分别记为![]() 、
、![]() 与
与![]() ,则
,则
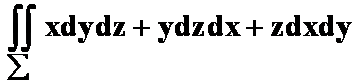 可化为二重积分( )
可化为二重积分( )
A.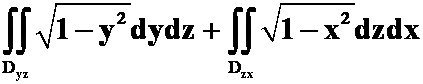 B.
B.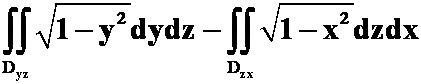
C.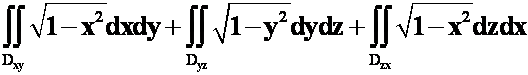
D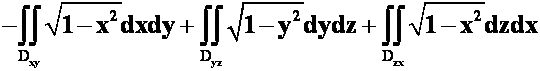
解 选 A
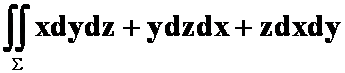
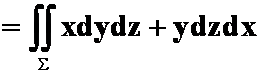
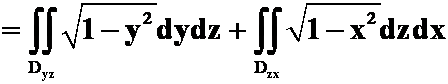
第9次作业第2题
设![]() 为抛物面
为抛物面![]() 介于平面
介于平面![]() 和
和![]() 之间的部分,则
之间的部分,则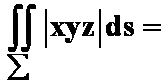
解 填 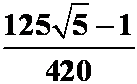
第9次作业第3题:
3.设![]() 是平面
是平面![]() 在第一卦限部分的上侧,
在第一卦限部分的上侧,![]() 是
是![]() 在
在![]() 面上的投影区域,则曲面积分
面上的投影区域,则曲面积分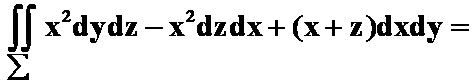 ( )
( )
A.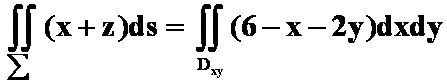
B.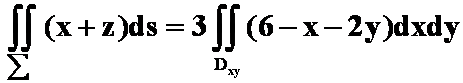
C.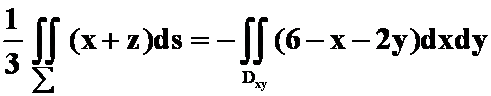
D.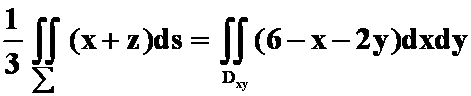
解 选D