第四次习题课
内容:第十章第一节至第三节
重点:两种类型的曲线积分的计算。格林公式。
难点:两种类型的曲线积分的联系、格林公式的应用。
专题:两类曲线积分以及二重积分的联系。

解释:三代一定:x,y,s代换,定限。
二代一定:x,y代换,定限。
定积分可以看做一种特殊的对弧长的曲线积分:弧为x轴。
定积分也可以看做一种特殊的对坐标(对弧长)的曲线积分:积分曲线为x轴正向。
例1:计算下列对弧长的曲线积分
(1)设![]() 是曲线
是曲线![]()
![]() 上对应于
上对应于![]() 的弧段,求
的弧段,求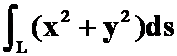 (第一次作业
)
(第一次作业
)
(答案:![]() )
)
(2)设![]() 为椭圆
为椭圆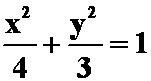 ,其周长记为
,其周长记为![]() ,求曲线积分
,求曲线积分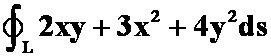 .(第一次作业)
.(第一次作业)
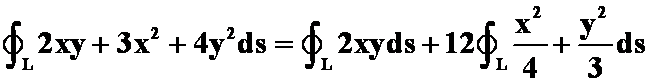
![]()
技巧1:利用求弧长;技巧2:利用对称性。
(3)计算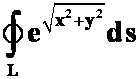 ,L为圆周
,L为圆周![]() 及x轴围成的在第一象限的闭区域的边界。
及x轴围成的在第一象限的闭区域的边界。
(答案: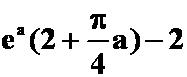 ,体会与第二类曲线积分的不同)
,体会与第二类曲线积分的不同)
例2:计算下列对坐标的曲线积分
(1)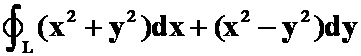 ,
,
其中![]() 是曲线
是曲线![]() 与
与![]() 轴所围平面图形的整个边界,按逆时针方向.(第二次作业)
轴所围平面图形的整个边界,按逆时针方向.(第二次作业)
(答案:4/3)
(2)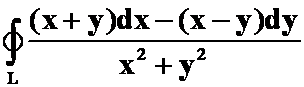 ,分别对下列封闭曲线求此积分
,分别对下列封闭曲线求此积分
<1>L为椭圆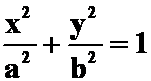 沿逆时针方向。
沿逆时针方向。
<2>L为圆周![]() 沿逆时针方向。
沿逆时针方向。
(答案:<1>![]() <2>0)
<2>0)
例3求柱面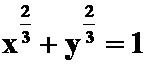 在球面
在球面![]() 内的侧面积.
内的侧面积.
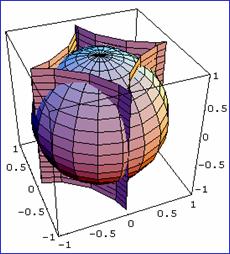
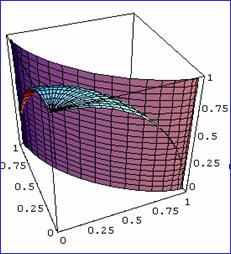
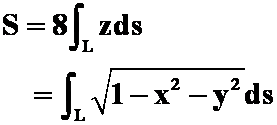
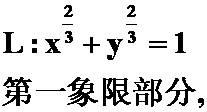
答案: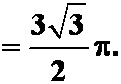
例4 利用曲线积分,求星形线
![]()
围成的面积。
(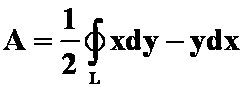 答案:
答案: ![]() )
)
专题:曲线积分与路径无关问题

利用与路径无关可以解决:
1.将复杂曲线积分变为简单曲线的积分。
2.闭区域积分简化运算。
3.求全微分的原函数。
注意:闭区域内被积函数是否有一阶连续偏导。
例5求
(1)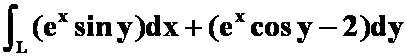 其中
其中![]() 为上半圆周
为上半圆周
![]() ,
,![]() ,
,
沿逆时针方向。
(直接利用与路径无关,答案:0)
(2)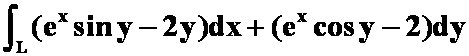
L同上。
(稍微改动后与路径无关,变简单曲线;答案:![]() 。)
。)
例6 利用格林公式,计算曲线积分
(1)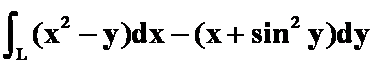
L是圆周![]() 从(0,0)到(1,1)的一段弧。
从(0,0)到(1,1)的一段弧。
(答案: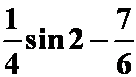 )
)
(2)曲线积分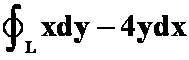 ,
,![]() 为圆
为圆![]() ,沿逆时针方向(据第三次作业修改)
,沿逆时针方向(据第三次作业修改)
(格林公式不一定非得在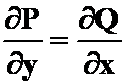 下才用!
下才用!
答案:5![]() )
)
例7 验证下列(2y+x)dx+(2x+y)dy在整个xoy平面内是某一函数u(x,y)的全微分,并求此函数。
(答案: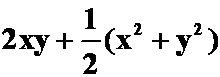 )
)
补充题:
1、设![]() 是点
是点![]() 与点
与点![]() 间的直线段,则曲线积分
间的直线段,则曲线积分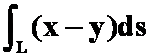 可化成定积分( )。
可化成定积分( )。
A.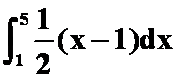 ;B.
;B.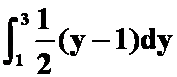 ;C.
;C.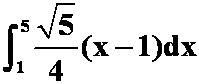 ;D.
;D.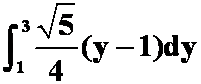 。
。
解 直线段AB的方程为: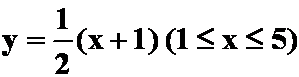
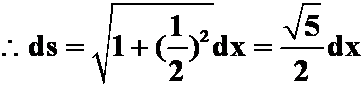
答案:C
2、设![]() 是抛物线
是抛物线![]() 上从点
上从点![]() 到点
到点![]() 的弧段,
的弧段,![]() 是二元连续函数,则曲线积分
是二元连续函数,则曲线积分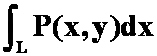 化成定积分( )。
化成定积分( )。
A.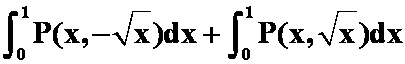 ;
;
B.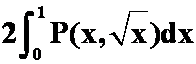 ;
;
C.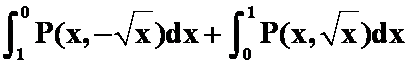 ; D.
; D.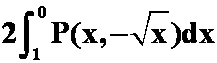 。
。
解 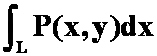
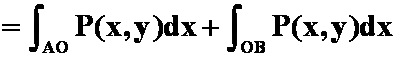
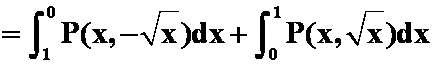
答案:C
3.设![]() 是螺旋线
是螺旋线![]() 上从
上从![]() 到
到![]() 的弧段,则
的弧段,则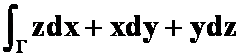 之值为( )。
之值为( )。
A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() 。
。
解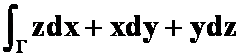
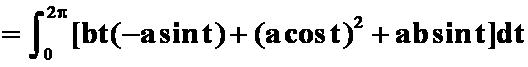
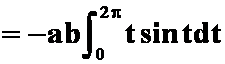
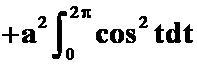
![]()
![]()
答案:A
4.以
![]() 为全微分的一个二元函数
为全微分的一个二元函数![]()
![]()
解 ![]()
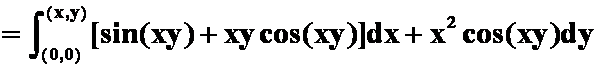
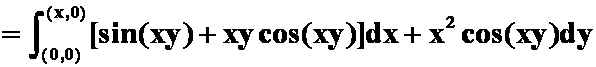
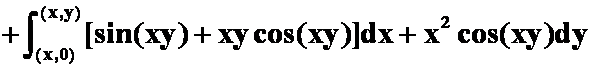
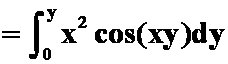
![]()
5设![]() 为圆
为圆![]() ,沿逆时针方向,则曲线积分
,沿逆时针方向,则曲线积分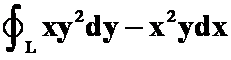 用格林公式计算时必出现的二次积分是
用格林公式计算时必出现的二次积分是![]() 。
。
A.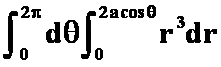 ;
B.
;
B.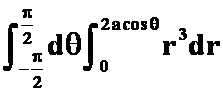 ;
;
C.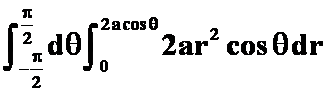 ; D.
; D.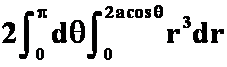 。
。
6.力场![]() 将一质点沿椭圆
将一质点沿椭圆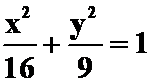 依正向移动一周,则
依正向移动一周,则![]() 所做的功是
所做的功是![]() 。
。
A.![]() ;B.
;B.![]() ;C.
;C.![]() ;D.
;D.![]() 。
。
解 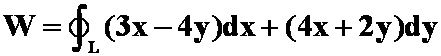
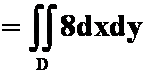
![]()