第三次习题课
内容:第九章第一节至第四节。
重点:重积分的概念、性质与计算。
难点:三重积分的计算、重积分的应用。
专题:重积分化累次积分的定限。
原理:用微元法先求面积,再求体积。相当于数次定积分。
定限方法:“扫描定限”(以二元为例)
原则:1)后积的定范围,先积的表示成后积的表达式。
2)扫描方式:
a)竖线横扫(X-型):先积y后积x。
b)横线竖扫(Y-型)。先积x后积y。
c)射线旋转扫(极坐标)
3)当上下限(左右限)函数表达式变化时进行分段。
注意事项:
1.关于如何选积分次序,它取决于三点:1).判断是X型还是Y型。2)尽可能不分块。3)考虑被积函数先积的变量积分更简单。
2.先画图,将交点和交线表示出来。图形不一定精准,但是大小位置不能错。
3.对于三元函数的积分,(1)可以“先二后一”或“先一后二”。平行xoy面截痕易表示的用先二后一,投影且上下两部分曲面易表示的用先一后二。
个人看法,如果两种都能用,最好还是用“先一后二”。 事实上它也用的比较多。
例1:求下列二重积分。
1、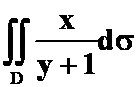 ,D:由
,D:由![]() 围成。(竖线横扫)
围成。(竖线横扫)
(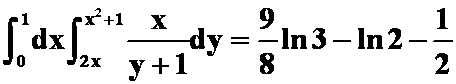 )
)
2、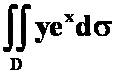 ,
,![]()
![]() 围成。
围成。
(竖线横扫:
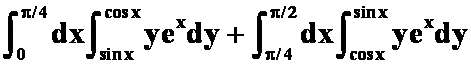
=![]() )
)
3、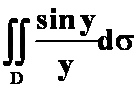 D:由y=2,y=x,y=2x围成。
D:由y=2,y=x,y=2x围成。
(横线竖扫:被积函数先积x更简单)
(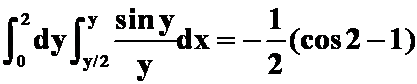 )
)
4、
(横线竖扫: 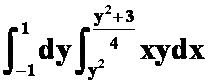 =0)
=0)
5、改变下列二重积分的积分次序
1)、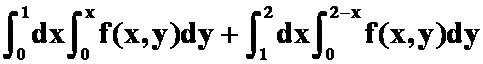
(答案: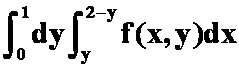 )
)
2)、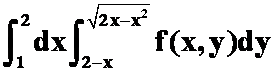
(答案: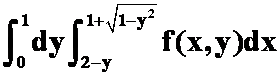 )
)
例2:求下列三重积分。
1、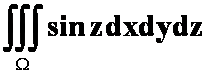 (
(![]() 为单页双曲面
为单页双曲面![]() 与
与![]() 围成。(先二后一)
围成。(先二后一)
(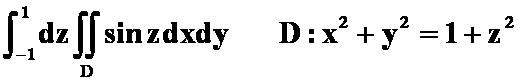 答案:0(也可以用对称性))
答案:0(也可以用对称性))
2、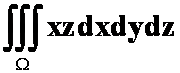 ,
,
![]() 围成。(先一后二)
围成。(先一后二)
(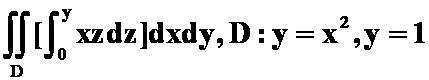 围成,答案:0)
围成,答案:0)
3、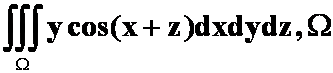 :抛物柱面
:抛物柱面![]() 及平面
及平面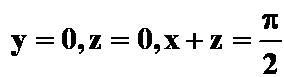 所围成的区域. (先一后二)
所围成的区域. (先一后二)
(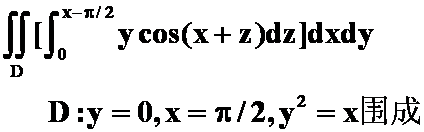
答案: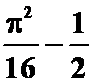 )
)
注意:关于三重积分,并不见得每一边界曲面都必须画得准确无误,先尽可能画准确常见的简单的曲面,对于较难画出的,有时只需知道投影或边界的范围。
![]()
4、求下列曲面所围成的立体体积:
![]() 及
及![]() (含有z轴的部分)
(含有z轴的部分)
(法1:二重积分
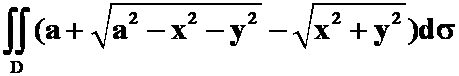 )
)
![]() 答案:
答案:![]()
法2:三重积分
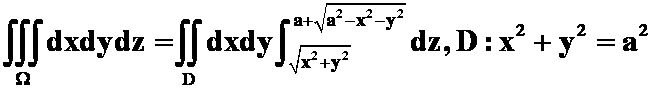
专题:化极坐标、球面坐标、柱面坐标问题。
1.对于二重积分化极坐标以及三重积分对于球面坐标与柱面坐标问题,一般用于被积函数或积分区域表达式含平方和的情形。柱面坐标相当于对x,y是极坐标,对z是直角坐标,球面坐标相当于完全是极坐标。注意扫描方式的不同。
2.柱面坐标实际上还是“先一后二”,只是后面的“二”将之化为二重的极坐标;球面坐标的扫描方式很特殊,先固定![]() ,先用射线定
,先用射线定![]() ,再对
,再对![]() 分别旋转扫描。
分别旋转扫描。
3.关于何时用柱面,何时用球面。一般原则是:当被积范围是柱体,用柱面;当被积范围是椎体、球体、椭球体等,用球面。
例3.将下列积分改为极坐标下的积分。
1、 D:
D:![]() (区域平方和)
(区域平方和)
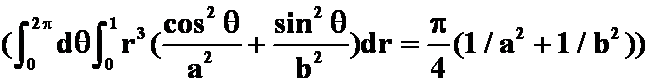
2、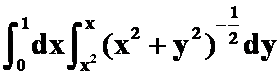 (被积平方和)
(被积平方和)
(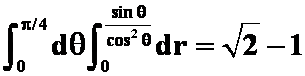
注意下面错误的定限: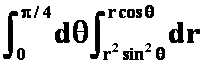 ,知道问题出在那里吗?)
,知道问题出在那里吗?)
3、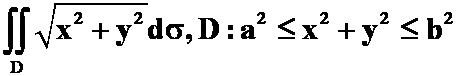 (环)
(环)
(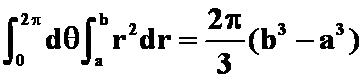 )
)
4、设平面薄片所占的闭区域D由螺线![]() 上的一段弧
上的一段弧![]() 与直线
与直线![]() 围成,它的面密度为
围成,它的面密度为![]() 。求这个薄片的质量。(97页16题)
。求这个薄片的质量。(97页16题)
(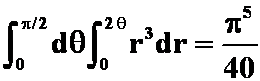 )
)
例4:用球面坐标或柱面坐标计算下列三重积分。
1、计算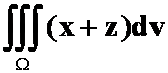
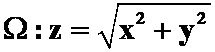 与
与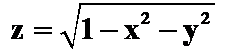 围成。(区域平方和,椎、球体)
围成。(区域平方和,椎、球体)
(球面坐标:(注意关于zoy对称)
 )
)
2、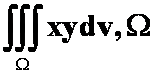 是由柱面
是由柱面![]() 及平面z=1,x=0,y=0围成的在第一卦限的闭区域。
及平面z=1,x=0,y=0围成的在第一卦限的闭区域。
(区域平方和,柱体,柱面坐标:
 )
)
3.计算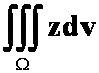 ,其中
,其中
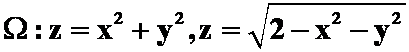 围成。
围成。
(柱面坐标: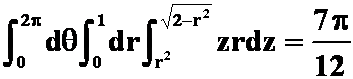 )
)
此题也可用球面坐标,但是需要分块,较麻烦。)
4.计算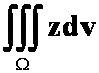 ,其中
,其中
![]()
(球、椎体;用球面坐标:
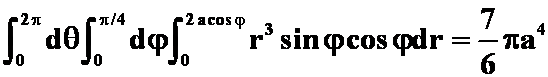 )
)
专题:关于重积分的证明题。
一般方法:1.交换积分次序。
2.二重积分与一重积分互换。
例5.证明与应用:
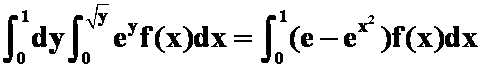
(提示:交换积分次序即可)
例6.证明:
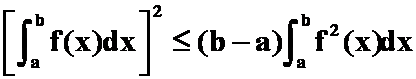
(提示:一重积分化二重积分)
应用题:
例7.求锥面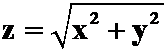 被柱面
被柱面![]() 所割下部分的面积。
所割下部分的面积。
![]() 答案:
答案: ![]() )
)
补充题:
1.把二重积分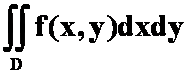 化为极坐标系下的二次积分为
,其中D由
化为极坐标系下的二次积分为
,其中D由![]() 与
与![]() 所围成。
所围成。
答案: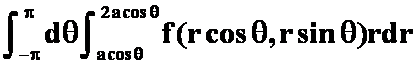
2.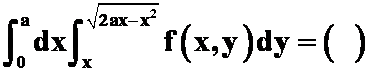 。
。
A.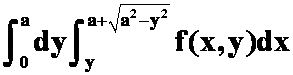 ;
;
B.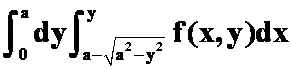 ;
;
C.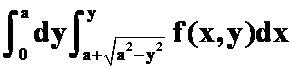 ;
;
D. 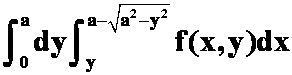 。
。
答案:![]()
3.设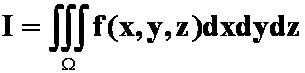 ,其中
,其中![]() 为
为![]() 及
及![]() 所围成的区域,用先二后一法化为下列积分,正确的是
所围成的区域,用先二后一法化为下列积分,正确的是
![]() 。
。
A.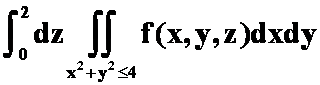 ; B.
; B.![]() ;
;
C.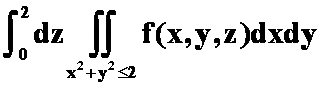 ; D.
; D.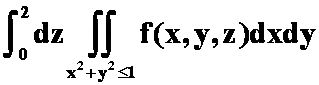 。
。
答案:B
4.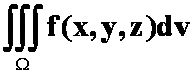 ,
,![]() 为
为![]() 所围成的区域,用先一后二法化为下列积分,形式正确的是
所围成的区域,用先一后二法化为下列积分,形式正确的是
![]() 。
。
A.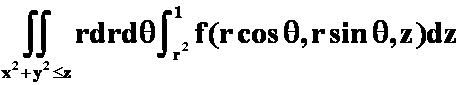 ;
;
B.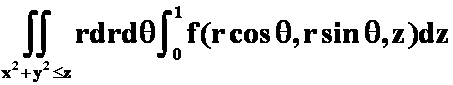 ;
;
C.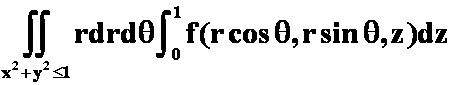 ;
;
D.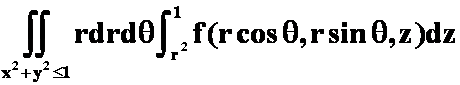 。
。
答案:D。
5把三次积分
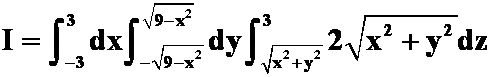 化为在球面坐标系下的三次积分为
。
化为在球面坐标系下的三次积分为
。
解: 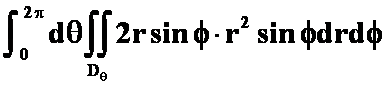
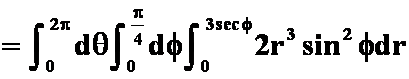
6. 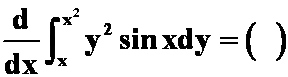
A.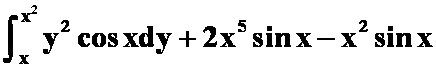 ;
;
B.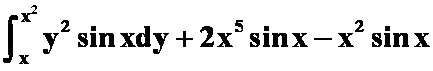 ;
;
C.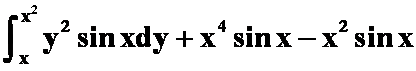 ;
;
D.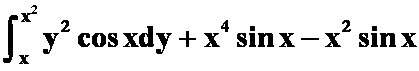 。
。
答案:A
7.把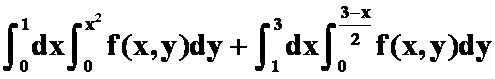 化为先x后y的二次积分为:
化为先x后y的二次积分为:
答案: