第二次习题课
内容:第八章第六节至第八节。
重点:多元函数的微分、多元函数的极值。
难点:方向导数与梯度。
专题:空间曲线与曲面的几何问题。
曲线的切线—与二元函数的偏导数有关。
曲面的切平面—与二元函数的微分有关。
例1.空间曲面的方程为
![]()
求其在点(1,1,1)处的切平面方程。用平面:![]() 截此曲面,求其交线在(1,1,1)的切线方程。并验证此切线在上述切平面上。
截此曲面,求其交线在(1,1,1)的切线方程。并验证此切线在上述切平面上。
(切平面:![]()
切线: 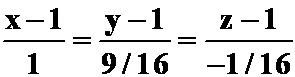 ,用参数方程代入验证。)
,用参数方程代入验证。)
例2.求椭球面![]() 确定的隐函数z=f(x,y)在点(1/2,1/2)的全微分。并求椭球面在点(1/2,1/2,1/2)的切平面方程。由此题可以得出什么结论?
确定的隐函数z=f(x,y)在点(1/2,1/2)的全微分。并求椭球面在点(1/2,1/2,1/2)的切平面方程。由此题可以得出什么结论?
(答案: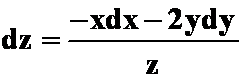 ,
,
在点(1/2,1/2)的全微分:![]() ,
,
切平面:![]()
结论:全微分确定的平面即为切平面。)
专题:多元函数极值与最值与一元函数极值最值的比较:
|
|
一元函数 |
多元函数 |
|
|
极值 |
必要 条件 |
驻点:
|
驻点:
|
|
充分 条件1 |
驻点+
( |
驻点+
(A<0极大,A>0极小)
( |
|
|
充分 条件2 |
驻点+左右单调性相反 |
--- |
|
|
最值 |
必要 条件 |
极值点或边界点 |
极值点或边界曲线上的点 |
|
充分 条件 |
闭区间连续函数所有极值点、边界点中的最大(小)值 |
闭区域连续函数所有极值点、边界线中的最大(小)值 |
|
|
充分 条件2 |
具体应用时唯一的驻点。 |
具体应用时唯一的驻点。 |
|
例3.求函数
![]() 在
在![]() 的极值与最值。
的极值与最值。
(内部:极大值![]() ;
;
边界线上的可能最值点:
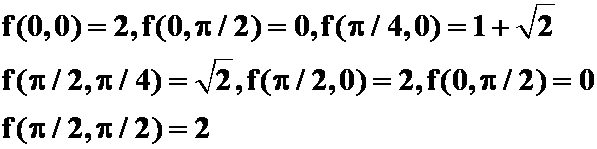 最大:
最大:![]() ,最小:
,最小:![]() ,
,![]() )
)
例4.求由方程
![]()
确定的函数z=f(x,y)的极值。
(驻点:(1,-1),此时z有两个值:6与-2,说明此方程确定两个函数分支,z=6的分支为极大值,z=-2的分支为极小值。)
例5.抛物面![]() 被
被![]() 截成一椭圆,求原点到椭圆的最长距离与最短距离。
截成一椭圆,求原点到椭圆的最长距离与最短距离。
(距离: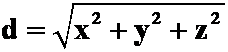 ,拉格朗日函数:
,拉格朗日函数:
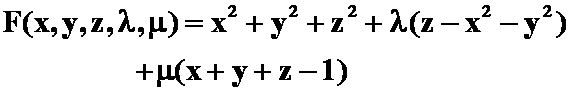 驻点:
驻点: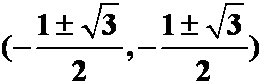 ;
;
最长: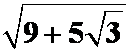 ,最短:
,最短: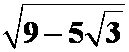 。
。
例6 求内接于半径a的球且有最大体积的长方体。
(拉格朗日乘数法,各边边长为![]() 时,体积最大,最大值为:
时,体积最大,最大值为: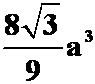 )
)
专题3 方向导数、梯度、偏导数与微分的关系。
可微![]() 有任意方向的方向导数
有任意方向的方向导数
方向导数![]() 偏导
偏导
方向导数![]() 梯度(值)
梯度(值)
等高线的方向![]() 梯度的方向
梯度的方向
注意:偏导、方向导数均是数量,梯度是向量。方向导数可以看作是梯度在此方向的投影。
例7.求函数![]() 在曲线
在曲线![]() 上点(1,1,1)沿曲线在该点的切线正方向的方向导数。并求此点梯度以及沿着梯度方向的方向导数。最后的结论说明什么?
上点(1,1,1)沿曲线在该点的切线正方向的方向导数。并求此点梯度以及沿着梯度方向的方向导数。最后的结论说明什么?
(切线正向:{1,2,3}, 方向导数: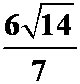
梯度:{2,2,2},方向导数:![]() 。此方向导数值即为梯度的模。说明梯度方向就是方向导数最大的方向。换句话说,梯度的模即为最大的方向导数。)
。此方向导数值即为梯度的模。说明梯度方向就是方向导数最大的方向。换句话说,梯度的模即为最大的方向导数。)
例8:(练习册)求函数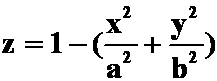 在点
在点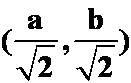 处沿曲线
处沿曲线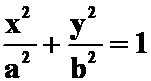 在这点的内法线方向的方向导数。
在这点的内法线方向的方向导数。
(答案: 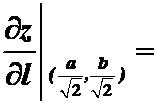
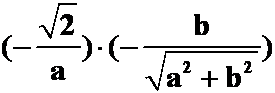
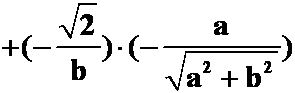
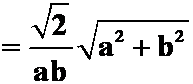 )
)
例9.在椭球面![]() 上求一点,使得函数
上求一点,使得函数![]() 在该点沿
在该点沿![]() 的方向导数为最大。
的方向导数为最大。
(设此点为(![]() )方向导数:
)方向导数: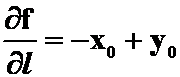
构造拉格朗日函数:
![]() 答案:最大值点:(-1/2,1/2), 最大值:1)
答案:最大值点:(-1/2,1/2), 最大值:1)
补充题:
1.求曲线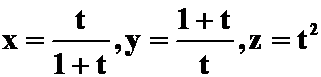 上的点,使
上的点,使
在该点的切线平行于平面![]() 。
。
解: 切向量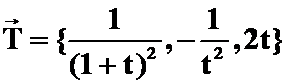
平面法向量![]() ,
,![]()
即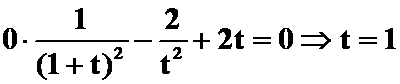 ,所求的点为
,所求的点为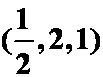 。
。
2.求曲面![]() 到平面
到平面![]() 的最短距离。
的最短距离。
解: 曲面![]() 上点
上点![]() 到平面
到平面
![]() 的距离为:
的距离为: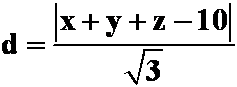 ,
,
因为![]() 与
与![]() 极大值相同,令:
极大值相同,令:
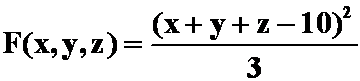
![]()
由
解得,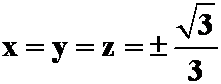
可能的极值点为:
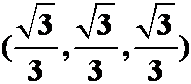 ,
,
比较得  。
。
3.设![]() 是由方程
是由方程![]() 所确定的隐函数,则当
所确定的隐函数,则当![]() 时,
时,![]() .
.
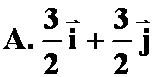 ;
; 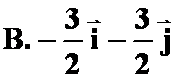 ;
;
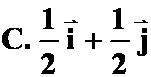 ;
;

(答案:D)