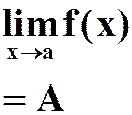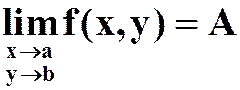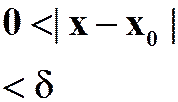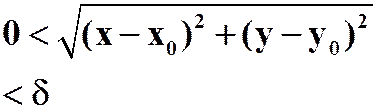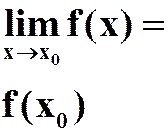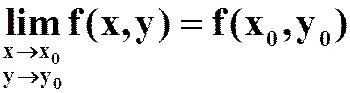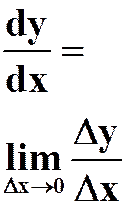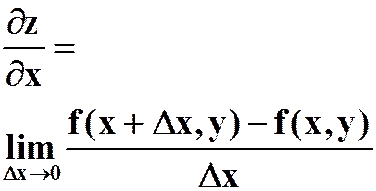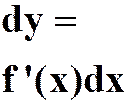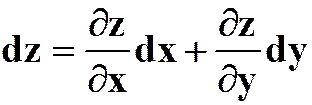第一次习题课
内容:第九章第一节至第五节。
重点:多元函数的极限与连续性、多元函数的偏导。
难点:多元函数极限的存在性。
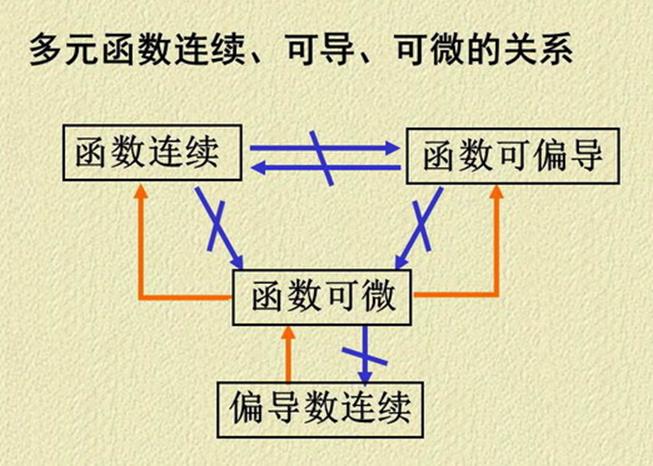
表:多元函数的极限、连续、偏导、微分与一元函数的对应概念的比较。
|
|
一元函数 |
多元函数(以二元为例) |
|
|
极限 |
公式 |
|
|
|
自变 量 |
|
|
|
|
连续 |
公式 |
|
|
|
联系 |
连续 |
连续 |
|
|
导 数 |
公式 |
|
|
|
联系 |
可导 |
可偏导与连续无必然关系 |
|
|
微分 |
公式 |
|
|
|
理解 |
以直线 代曲线 |
以平面代曲面 |
|
|
联系 |
可微
可微 |
可微 可微 偏导连续 |
|
专题1 多元函数的极限问题
多元函数的极限的判断较为复杂,但是也可以总结出一般的原则:多个变量的问题尽可能变成“单个变量”的问题。即“整体代换法”。然后求一元函数的极限的方法可以完全移植过来。
例1 求下列二元函数的极限。不存在的说明原因。
(1)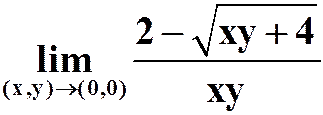
提示:xy看成一个整体。
答案: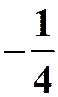 。
。
(2)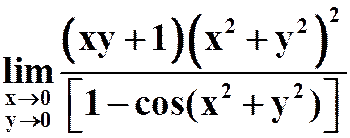
提示:![]() 看作整体。
看作整体。
答案:2.
(3)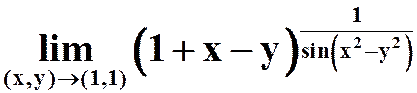
提示:重要极限。x-y作为整体。
答案:![]()
(4)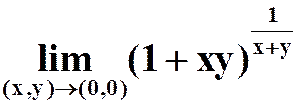
问:能否:
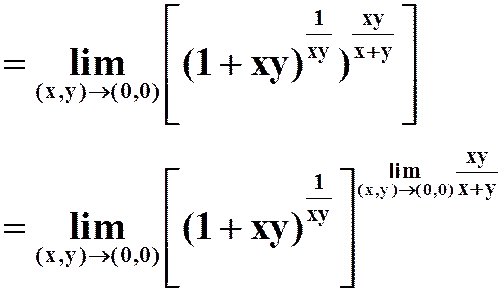 ?
?
说明原因。
提示:1)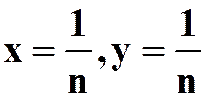 趋于1
趋于1
2)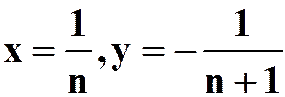 趋于
趋于![]() ;
;
答案:不存在.
(5)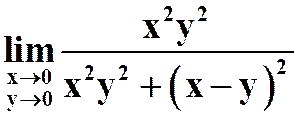
提示:分别沿着y=x及y=2x。
答案:不存在。
例2 判断下列函数在(0,0)点的连续性和是否可偏导,是否可微。
(1)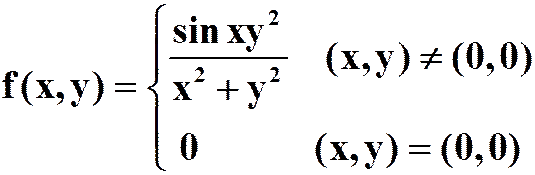
答案:连续,有偏导,不可微。
(2)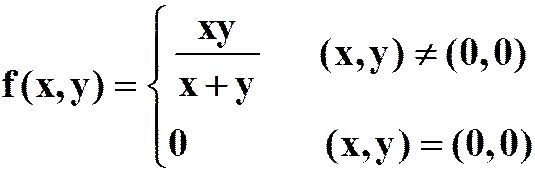
答案:不连续,有偏导,不可微。
专题:多元函数求导(偏导)的原则。
标准公式:
![]()
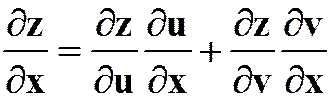
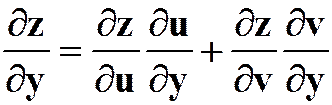
方法:遍历有向链法。
1.
遍历有向链法的原理
根据多变量处理的“逐一处理”以及“逐级处理”的原则
2.
遍历有向链法的具体操作步骤
用人伦关系比喻变量之间的关系.
关于求导及求偏导
1) 罗列所有变量,变量之间用有向线段相连,各有向线段的箭头由“父亲”指向“儿子”,最终形成一个有向链图.
2) 若需要求某个导数(偏导),由此导数(偏导)式中分子对应的变量开始,到分母对应的变量终止,按有向链图的箭头方向逐级遍历(即所有路径都走一遍,不重复、不遗漏)所有的路径.每一条路径用一项表示,同一项中每经过一步写一个导数(或偏导)式作为其因子,然后将各种路径对应的项相加.
3) 所有式子中,若分子与分母之间无“旁系亲属”(即分子对应变量的后代中不存在分母对应变量的“兄弟”或旁系“长辈”)则写成导数形式,否则写成偏导形式.
x
如以下的w对t必须写成偏导形式
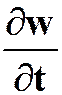 :
:

要点与注意事项
1)因变量在第一列,中间变量在第二列,自变量在第三列。(有的变量既作中间变量,又作自变量,因此可据情况占几个位置)
2)项数取决于中间变量的个数。
3)每一项的因式个数取决于每一单链的“长度”。
例3 求下列函数的偏导
(1)![]() ,
,![]() ,求
,求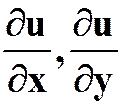 。
。
提示:注意x的地位。
答案: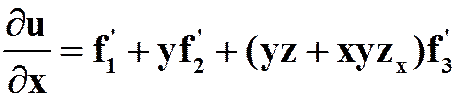
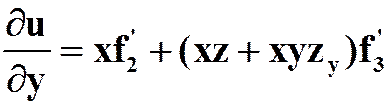 )
)
(2)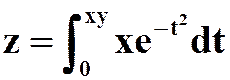
答案: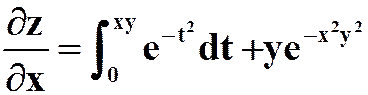 ,
,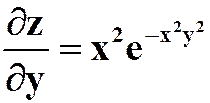 ;
;
(3)设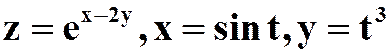 ,求
,求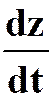
答案: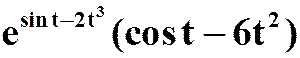 )
)
(4)设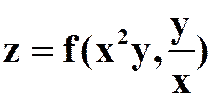 ,
,![]() 有二阶连续偏导,求
有二阶连续偏导,求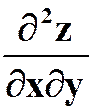 。
。
答案: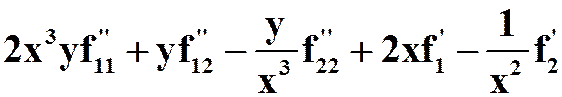
(5)设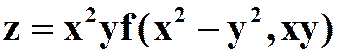 ,其中f有连续偏导数,求
,其中f有连续偏导数,求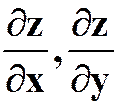 。
。
答案: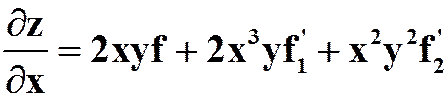
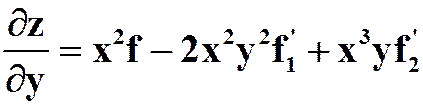
(6)设![]() 具有二阶连续偏导数,且
具有二阶连续偏导数,且
满足 ,
,
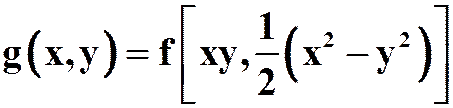 ,
,
求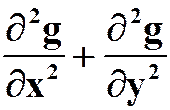 .
.
答案:
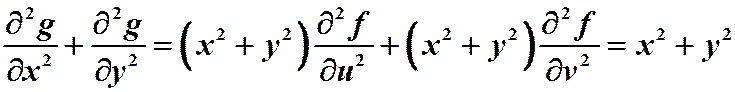 注意:二阶偏导的有向链图“换头不换身”
注意:二阶偏导的有向链图“换头不换身”
例4 求下列隐函数的偏导
提示:隐函数的偏导原则:一个方程解一个“未知量”。
(1)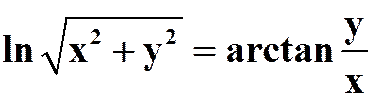
答案: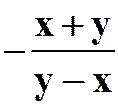
(2)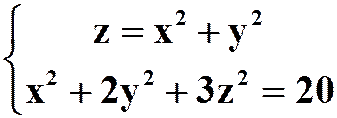 ,求
,求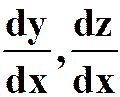
提示:必须先搞清变量之间的关系。
答案: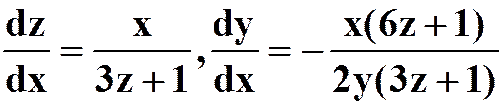 )
)
(3)设![]() 是由方程
是由方程
![]()
所确定的二元函数,求![]() 及
及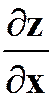 。
。
提示:直接用微分做更简单,但概念要清楚。要灵活利用“微分形式的不变性”。就是求“d”时不需要去管变量是自变量、中间变量还是因变量。
(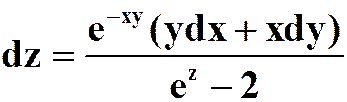 ,
,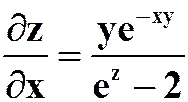 )
)
(4)设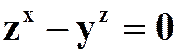 ,求
,求![]() .
.
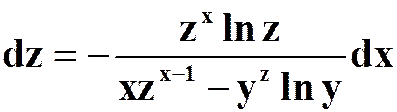
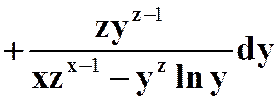 .
.
补充题:
1.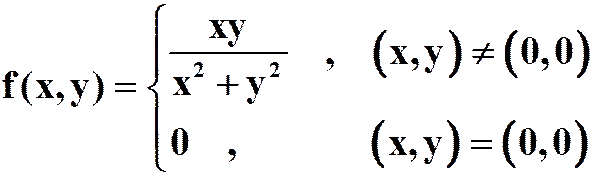 ,则
,则![]() 在点
在点![]() 处
( )
处
( )
A.连续,且偏导数存在;B.不连续,但偏导数存在;
C.连续,但偏导数不存在;D.不连续,但偏导数不存在。
答案:![]()
2.设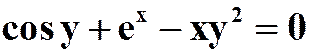 ,则
,则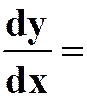
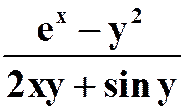 。
。
3.设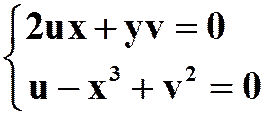 ,求
,求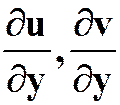 。
。
解:方程两边对![]() 求偏导数得:
求偏导数得:
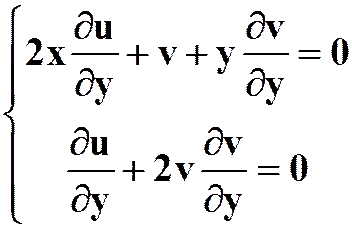
解得,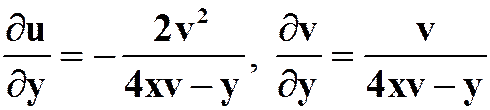
4.设![]() 且
且![]() ,其中
,其中![]() 具有二阶连续偏导数,求
具有二阶连续偏导数,求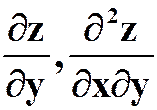 。
。
解: 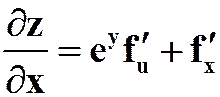 ,
, 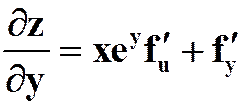
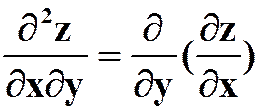
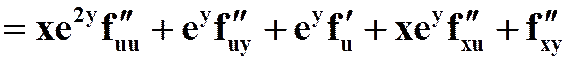
5.对函数![]() 在点
在点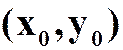 来说,下列说法
来说,下列说法
正确的
( )。
A.若函数在该点的极限存在,则函数在该点连续;
B.若函数在该点的两个偏导数存在,则函数在该点连续;
C.若函数在该点的全微分存在,则函数在该点连续;
D.以上说法都不正确。
答案:C