三等分任意角挑战世界
方和生、方祖旺
湖南省吉首市龙山县石牌镇玉河村六组,416804
摘要:用正方形三等分和圆弧三等分求得角的三等分。
关键词:圆规、直尺、三等分点、三等分线。
前言:古希腊三大几何问题之一,纪元五,六百年间希腊的数学家们就已经想到了二等分任意角的方法,而三等分任意角就成了多年的数学难题,那些数学家都证明此问题不能完成。我有一种方法发此论文证明。
三等分任意角:
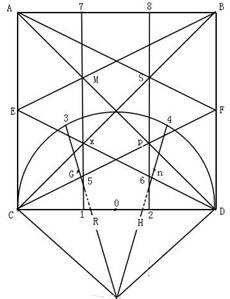
用圆规和没有刻度的尺,来证明任意角的三等分,先证明一个正方形的三等分原理,用圆规定在角心,以适当的长度找出角两边相等长的点C和D,再把C,D连接,再找出C、D的中点,用圆规定在C点和D点以适当大的圆,以这两个圆的交点与角心连接,等于角的二等分,也是C、D的中点O,以C、D为正方形的边长向上画一个正方形,用圆规以C、D长度为半径,分别定在C点O点和D点往上找出正方形的各端点,再从角心至O点向上延长到W点,再用圆规以C、O长度为半经,定在W点找出了正方形的A点和B点,再以适当大的圆分别定在A、B、C、D点找出AC和BD的中点E和F,再把AF连接,AD连接,BE连接,BC连接,CF连接,DE连接。(如图一):在图内交叉点分别得出m,x,s,p点,再把mx连接至正方形边线,sp连接至正方形边线。这两条线就是正方形的三等分线,1点和2点就是直线的三等分点。
下面再找出最大角度圆弧的三等分点,用圆规定在O点,从C往上圆至D点,成为一个半圆图形,再找出半圆弧长的三等分点,因为半径的长度是任意一个圆内的六边形边长。所以用圆规定在C点以CO的长度找出了弧长的三等分3点和4点。3点和4点是最大角度的三等分点,1点和2点是最小角度的三等分点,也是直线的三等分点。再从最大角度弧长三等分点3连接到5点,再用虚线从5点延长到CD的直线上R点,又从最大角度的弧长三等分点4连接到6点,用虚线从6点延长到CD的直线H点,再用圆规和直尺找出3点到R点直线上的中点G。又找出4点到H点直线上的中点n,把G点和1点连接,n点和2点连接,再把3点G点1点这三个点连接成弯曲线,又把4点n点2点这三个点连接成弯曲线,这两条弯曲线就是任意角度弧长的三等分线,任意角的弧线通过两条三等分线的交点,这两个点就是任意角度和弧长的三等分点。
论证:三等分定理图的来历,由任意角的二等分点和正方形三等分直线的三等分,再加上半圆弧长三等分及等分线组合而成。图中每个定点都是用圆规和没有刻度的直尺从交点、中点、三等分点组合而成。最后得出图论为:
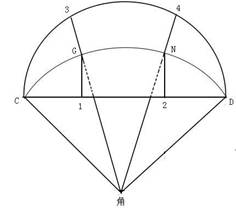
任意角九星定理图。由这种方法求来的三等分答案是,角的边长相等,弧长等分,角度相同。
后语:发此论文理由有三,一:贡献国家、二:展示作品、三:挑战世界,若有不同的理论和方法,欢迎讨论和指正。
论无解方程
方和生 方祖旺
湖南省龙山县石牌镇玉河村六组 湖南吉首 416800
摘要:本文主要以传统文化和民间文化论述了一些实践知识及各种不同的运输方法
关键词:分段
传递 连接 往返 数学断奇案
前言:中国文化博大精深,只要把史上、传统及民间文化三者结合,很多难题即可迎刃而解;那为何还有十万个为什么呢?那是教育只重视史上文化,把其他文化称为脑筋急转弯和渡婆婆客帐。没有理论的解题法,其实理论不如实践,实践能证明一切;下面用文章来论证:理论是纸上谈兵,实践是常胜将军
一:分段方程。
某地有108吨货,用船、大车、小车共36辆运往某地。船运12吨,大车装9吨,小车装1吨,问船、大车、小车各用多少辆。注:未知数不用0
解曰:此题用史上的方程不能完成,得用分段方程。设这货起点为我家乡:湖南省龙山县石牌镇玉河村6组,有108吨百合,设运货终点为台湾,在这种地理条件下,方程无法解题,为什么?因为这是史外、民间传统文化,只有用分段方程才能解决,小车运小路,大车运国道,船运海峡。先把小车的可用数找出来,36辆运3次为108,27辆运4次为108,18辆运6次为108,12辆运9次为108,9辆运12次为108,4辆运27次为108,3辆运36次为108。再把大车的可用数找出来。12辆运1次为108,6辆运2次为108,3辆运4次为108,2辆运6次为108。还要把船的可用数找出来。9辆运1次为108,3辆运3次为108,1辆运9次为108,就在这些可能数里面找出船3辆加大车6辆加小车27辆等于36辆,先用27辆小车分4次从起点运往国道,再用6辆大车分2次从国道运往福建,然后用3条船分3次从福建运到台湾,在这种地理条件下是唯一的解题方法,否则就是世界难题
二:传递方程
某地有36块砖,用男、女、小孩共36人搬往某地,男搬4、女搬3、小孩3人抬1块。问男、女、小孩各多少人。注:未知数不用0
解曰:这个题用史上的方程也是无解题,只能用传递方法是民间通常用的搬运方式,而史上没有记载,所以成了难题,要用传递排队的方式破解此题,只要知道方法,可以找出8种排队方式解题
一:32个男人、1个女人、3个小孩。二:28个男人、2个女人、6个小孩。三:24个男人、3个女人、9个小孩。四:20个男人、4个女人、12个小孩。五:16个男人、5个女人、15个小孩。六:12个男人、6个女人。18个小孩。七:8个男人、7个女人、21个小孩。八:4个男人、8个女人、24个小孩
排队方法:一个男人一个位,一个女人加三个小孩,每次传4块砖,分9次传完36块砖,在这8个不同的答案当中,只有排队的位置多少和男、女、小孩的人数不同,而传法是一样的,都是每次传4块砖,分9次传完36块砖,从一个无解的题中得出了8个不同的答案来,欢迎大家参考!
三:连接方程
某部队有93人,在行军途中隔了一条河,自己造了4条船渡河,首长规定每船只装单人数,每船次数相等,问每船各装多少人
解曰:大家学的知识一定解不了此题。怎么办,不要急。设河有
四:往返方程
数学断奇案:从前有一富翁,他病危时写下遗书如下:我有108颗珍珠,有儿、孙、重孙共36人,大儿子种田,小儿子做官,其中儿子经商,因条件不一,分的多少不等。请分官叫我的儿、孙、重孙把108颗珍珠从库里搬出来,儿搬12颗,孙搬9颗,重孙搬1颗;请分管说出我有儿、孙、重孙各多少人?答对你就当我分官,即送你9颗珍珠。分法如下:用三个分具分为甲、乙、丙。长房分39颗,甲分具用三次,乙分具用两次,丙分具用一次。二房分34颗,甲分具用两次,乙分具用三次,丙分具用一次。三房分26颗,甲分具用一次,乙分具用两次,丙分具用三次。问:甲、乙、丙分具各装多少颗珍珠?
解曰:此题用方程不能完成,要用传递方程解决。先找出各种排队方法:一、32个儿子,1个孙子,3个重孙;二、28个儿子,2个孙子,6个重孙;三、24个儿子,3个孙子,9个重孙;四、20个儿子,4个孙子,12个重孙;五、16个儿子,5个孙子,15个重孙;六、12个儿子,6个孙子,18个重孙;七、8个儿子,7个孙子,21个重孙;八、4个儿子,8个孙子,24个重孙;经各种排队法得出八个结果。他家的最佳人数应该是:4个儿子,8个孙子,24个重孙;他有4个儿子,而又只分给三房,怎么解释?这个问题放在后面再论证,先把珍珠搬出来说;排队方法为12个位值,一个儿子占一个位得4个位,后面的位值是一个孙子加3个重孙,一次传12颗珍珠,分9次传完,这样就完成了第一步;分法如下:用往返方程,设:甲分具为10,乙分具为5,丙分具为1;长房分39颗,甲分具分三次得30,乙分具分两次得10;30+10=40。再用丙分具退回一次,等于(30+10)-1=39. 二房分34颗,甲分具分两次得20,乙分具分三次得15;20+15=35,再用丙分具退回一次,等于(20+15)-1=34;还有35颗珍珠,三房等于35-9,用甲分具分出一次得10,用乙分具分出一次得5,再用乙分具分回一次得5;等于10+5-5=10;再用丙分具分出一次,再用丙分具分回两次,等于10+5-5+
论证:这位老人是一个绝世高人,他明明有四个儿子,只给三个大儿子分,谁又敢来当这个分官呢?这就是老人的玄机,其实那9颗珍珠是给小儿子的,因为只有他才能分下去,别人是无法分的,也不敢来当这个分官,他想试探小儿子做官的能力,看是不是心如明镜的清官,后来小儿子把遗书一看,父亲把他排持到一边,不理解父亲的一番苦心,一言不语离开了,造成了一个僵局,所以后来无人当得下来这个分官,造成了现在的数学断奇案的故事。
结语:以上所述,为我国的文化快速进步,收集了一些史外知识,让大家作参考资料,希望论证,欢迎批评和指正!
作者简介:方和生,生于(1963-),男,湖南省龙山县石牌镇玉河村6组
方祖旺(1998-),男,湖南湘西龙山石牌镇;石牌中学
分解三大几何问题,立方倍积和化圆为方
方和生、方祖旺
湖南省吉首市龙山县石牌镇玉河村六组416804
摘要:通过多种定理综合论证论点,得出了立方倍积和化圆为方的结论。
关键词:三等分、五等分、尺规作图、原始定理。
引语:古人设局后人破,历史年代两千多,有缘千年来相会,尔等公开来演说。历史教育的名人,不要随便下结论,明明有解说无解,乱开金口误事情。历史擂台天下摆,人人个个不理解,多种定理来结合,可以破解圆方角。
一:用圆规和没有刻度的直尺来证明立方倍积。有四种方法。
第一种是很简单的方法:在任意一个正方体或长方体中只增加长度一倍,宽度不动,高度不动,等于两个同样大的立方体合在一起,这种方法只是提一提,并不是解题的关键。
第二种是稍难度方法:在任意一个正方体或长方体中,只增大长度和宽度,高度不动。在任意一个正方体或长方体的平面上,用直尺对角画两条对角线,再用圆规分别定在四角点从对角线的交点圆至正方形外找到圆线的交点,再把正方体外圆的四个交点,用直尺连接成外围正方形。又把长方体外围的四个圆线交点,用直尺连接成外围平行四边形,这两种图形的立方倍积以形成
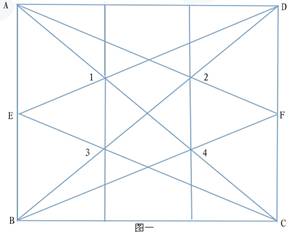
第三种是高难度方法:在任意一个正方体或长方体中,长度、宽度、高度同时增大,这种方法要找出一种立方倍积的原理:用很多小方块棋子,摆成两个同样大立方体,把这个立方体加在那个立方体上。要使长、宽、高同时加大而成一个完整的立方体,此图样就是立方倍积原理,这个原理是怎样发现的呢。我是用这些棋子由少到多,从小到大,一直用到60个棋子时,终于形成了规律,这个立方体长5个棋子,宽3个棋子,高4个棋子,一共60个棋子,再把这个立方体长加五分之一,宽加三分之一,高加四分之一,恰好加了60个棋子,就成了原来这个立方体的倍积,这个原理虽然出来了,但受条件限制,因为只能用圆规和没有刻度的直尺来论证论点找答案,所以还得找出二等分、三等分、五等分定理才能得出结论,下面就找出各等分定理。二等分定理:用圆规定在直线的两端以适当大的圆,得出两个圆线的交点,再用直尺把两个交点连接,就得到了二等分定理,再重复一遍就是四等分定
理了。三等分定理:(图一)
要先找出正方形三等分原理,用尺规作图画一个正方形A、B、C、D,再用二等分定理找出AC的中点E和BD的中点F,再把AF连接,AD连接,BF连接,BE连接,DE连接,CF连接,图内几个交点分别为1、2、3、4点。把1点和3点连接至正方形边线,再把2点和4点连接至正方形边线,这两条连接线就是正方形的三等分线,这样直线三等分就形成了。
再找出直线五等分定理:(图二)
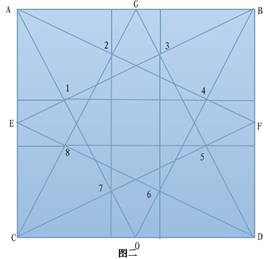
用尺规作图画一个正方形A、B、C、D,再用二等分定理找出AC的中点E,AB的中点G,BD的中点F,CD的中点O,再把AO连接、AF连接,BE连接,BO连接,CG连接,CF连接,DE连接,DG连接。图内分别得出需要的8个交点为1、2、3、4、5、6、7、8,把1点和4点连接至正方形边线,8点和 5点连接至正方形边线,2点和7点连接至正方形边线,3点和6点连接至正方形边线,这样就得出了任意直线的五等分点,定理证明:在任意一个正方体或长方体中再把它的长宽高同时加大的情况下,把它的长度用五等分定理加长五分之一,宽度用三等分定理加宽三分之一,高度用两次二等分定理加高四分之一,这个立方体就是原立方体的倍积了。
第四种方法是圆立方倍积:圆立方体长度不动,只加大直径和周围,在任意一个圆立方体中,分东西南北画两个垂直的直径,再把东西南北连接成正方形。这正方形边长就是该圆立方倍积的半径,也可以算式表示:半径的平方加半径的平方开根的数就是圆立方倍积的半径。
二:用尺规作图化圆为方
在任意一个圆图中,垂直画两个直径,用二等分定理把四个半径线段分成四等分点,把各半径加长四分之一,再用直尺从各定点连接正方形,这个正方形面积与圆的面积是最接近的,在化圆为方这个问题上,只是接近数,没有绝对精确,因为圆周率有一定的误差。用圆规和没有刻度的直尺来证明化圆为方,这种方法是唯一最接近的规律,若对圆周率有疑问,请上百度搜索《圆周开弓定理》
后语:我不知该不该发这篇文章,也不知道能不能发表成功,因为论
作者简介:
1.方和生;性别:男;1963,湖南省吉首市龙山县石牌镇河村六组;
2.方祖旺;性别:男;1998,湖南省吉首市龙山县石牌中学。
主题:论圆周率
前言:
我国魏晋时期的数学家刘微和南朝时期的数学家祖冲之,他们用割圆术求来的圆周率,他们为什么不把计算过程讲清楚呢?而设一个密率,让后人成了一个迷,二位数学家真是高人,他们也知道这个计算过程中有很多的问题,但又无法纠正,所以设了一个密率,让后人无法理解,我现在找出了圆本身的定理,又发现了祖冲之的计算过程,并且找出他错误的原因,所以发了这篇论文。

第一章
怎样计算圆周率:
用十位数的计算机,在10000直径的圆图里,用圆内接正多边形来求圆周率,把这个圆图分东西南北垂直画两个直径,成为四个相等的直角,先求四边形的边长,用5000的平方+5000的平方等于开根得7071.067812,这就是四边形边长,计算八边形边长先用四边形边长除以2,也就是7071.067812/2。在这个数的中点到圆心再画一个5000的半径,形成了两个直角三角形,一个在内,一个在外,先求内三角形,已知第一个边是3535.533906,已知第二个也是5000,用5000平方减3535.533906,平方等于开根得3535.533906,再求外三角形,已知一个边是:3535.533906,已知二个边是:5000-3535.533906=1464.466094。用3535.533906平方加1464.466094平方等于开根得出八边形边长是:3826.834324。用这样的方法反复的计算下去,反复的除以2,平方和开根,一直求到与圆线同体,无数可算为止,下面的各边数就不详细讲了。
16边长=1950.90322,它的内三角形边长是:已知B边长是:5000,已知C边长是:1913.417162。求得A边长是:4619.397663。外三角形边边长是:已知D边长是:380.602337,已知C边长是:1913.417162;求得E边长是:1950.90322。
32边长=980.1714032。它的内三角形边长,已知B边长是:5000,已知C边长是:975.45161。求得A边长是:4903.926402。它的外三角形边长,已知D边长是:96.073598,已知C边长是:975.45161。求得E边长是:980.1714032。
64边长=490.6767432。它的内三角形边长,已知B边长是:5000,已知C边长是:490.0857016。求得A边长是:4975.923633。它的外三角形边长,已知D边长是:24.076367,已知C边长是:490.0857016。求得E边长是:490.6767432。
128边长=245.4122852;它的内三角形边长:已知B边长是:5000,已知C边长是:245.3383716。求得A边长是:4993.977281。它的外三角形边长:已知D边长是:6.022719,已知C边长是:245.3383716,求得E边长是:245.4122852。
256边长=122.7153828;它的内三角形边长:已知B边长是:5000,已知C边长是:122.7061426,求得A边长是:4998.494093。它的外三角形边长:已知D边长是:1.505907,已知C边长是:122.7061426,求得E边长是:122.7153828。
512边长=61.35884648;它的内三角形边长:已知B边长是:5000,已知C边长是:61.35769142,求得A边长是:4999.623509;它的外三角形边长:已知D边长是:0.376491,已知C边长是:61.35769142,求得E边长是:61.35884648。
1024边长=30.67956763,它的内三角形边长:已知B边长是:5000,已知C边长是30.67942324,求得A边长是:4999.905876;它的外三角形边长:已知D边长是:0.094124,已知C边长是:30.67942324,求得E边长是:30.67956763。
2048边长=15.33980186;它内三角形边长:已知B边长是:5000,已知C边长是:15.33978381,求得A边长是:4999.976469;它的外三角形边长:已知D边长是:0.023531,已知C边长是:15.33978381,求得E边长是:15.33980186。
4096边长=7.669903186;它的内三角形边长:已知B边长是:5000,已知C边长是:7.66990093,求得A边长是:4999.994117;它的外三角形边长:已知D边长是0.005883,已知C边长是:7.66990093,求得E边长是:7.669903186。
8192边长=3.834951875;它的内三角形边长:已知B边长是:5000,已知C边长是:3.834951593,求得A边长是:4999.998529;它的外三角形边长:已知D边长是:0.001471,已知C边长是:3.834951593,求得E边长是:3.834951875。
16384边长=1.917475973;它的内三角形边长:已知B边长是:5000,已知C边长是:1.917475938,求得A边长是:4999.999632;它的外三角形边长:已知D边长是:0.000368,已知C边长是:1.917475938,求得E边长是:1.917475973;
在10000直径的圆内,由圆内正多边形求到16384个边时,大约接近了圆线。每个边用了25个三角形,16384边乘以25个三角形=409600个三角形,边数乘以边长=16384乘以1.917475973=31415.92634,化为1直径的圆等于3.141592634,用十位数的计算机只精确到八位数,后面的数要精确,得用多位数计算机计算,为什么要用10000直径的圆求呢,因为圆周率求得越大越精确,所以刘微他的圆求小了,数字位数用少了。
第二章
评论圆周率:
以上的这种计算过程和方法,给了我修改圆周率的一个充分理由,在求一个最小的边长里,用了25个三角形,有两个三角形是百分之百的精确,有23个三角形出现了问题,因为已知任意两个边求第三个边得数不还原,问题出现在开根和平方,因为只用十位数的计算机,开根平方都没把数算完,所以造成不还原的结果,最重要的是用5000减内三角形的那个A边,A边是开根的边,开根有余数,造成外三角形那个D边就长,这个边一长把整个周长就计算长了,至于勾股定理,它只能在某些数字中是百分之百的精确,比如说:勾3股4弦5,在很多数字中都是永不循环的小数,所以不能用勾股定理成千上万次的计算圆周率,这种计算结果造成一错在错千错万错,但有些问题又只能用勾股定理,才有答案,最后结论只有一个,勾股定理只能计算直角三角形,圆必须找出圆它本身的定理。
第三章
圆周开弓定理:
论点:在任意一个圆图中,以半圆周长为弓,半径DO为箭,直径AB为弦,射箭的时候开弓到什么位置才能使弦的长度加上箭的长度等于弓的长度,就用圆规定在D点从AO的中点F圆至BO的中点M,求得DO的延长点X,X点就是开弓的定点,再把AX连接,BX连接,半圆周长=AX+BX+DX,圆周长=2(AX+BX+DX)。
用开弓定理求圆周率:
以10000直径的圆图来求圆周率,先DF连接,DOF成为直角三角形,已知DO=5000,OF=2500,5000平方+2500平方=开根得5590.169944. DF=5590.169944,因为用圆规定在D点从F圆至M,所以DF=DX=5590.169944. OX=5590.169944-5000=590.1699438.再求AX和BX长度,AOX是直角三角形,BOX也是直角三角形,AOX=BOX。只要求AOX这个三角形,已知AO=5000,OX=590.1699438, AX=5000平方+590.1699438平方=5034.709581。定理证明C=2(AX+BX+DX)
C=2(5034.709581+5034.709581+5590.169944).
C=2*15659.58911.
C=31319.17821
化为一直径的圆=3.1319178…..
这是用十位数计算机算的,只精确到八位数,这种计算方法在一个圆内只用六个直角三角形,再不精确也比割圆术的精确,因为它用了四十多万个三角形。
论证
只要画一个
最后
请大家认真阅读及参考,希望大家论证,欢迎评论。如有不同看法可给予意见及指正!
作者:方和生