第五章 二次型习题
基本题
一、填空题
1.实二次型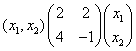 的矩阵为 ,秩为 ,正惯性指数为
,规范形为 .
的矩阵为 ,秩为 ,正惯性指数为
,规范形为 .
2.与对称矩阵合同的矩阵只能是
矩阵。
3.复二次型![]() 的规范形由 所唯一确定。
的规范形由 所唯一确定。
4.实二次型![]() 正定
正定![]() ,i=1,2,…,n.
,i=1,2,…,n.
5.实二次型的正惯性指数为![]() ,负惯性指数为
,负惯性指数为![]() ,秩为
,秩为![]() ,符号差为
,符号差为![]() .
.
(1) 已知![]() ,
,![]() 则
则![]() ,
,![]() ;
;
(2) 已知![]() ,
,![]() 则
则![]() 。
。
6. ![]() 的矩阵为 。
的矩阵为 。
7. 两个实二次型等价的充分必要条件是 ,两个复二次型等价的充分必要条件是 。
8. 任意满秩的3级实对称矩阵与且仅与下列对角矩阵之一合同: .
二、判断题
1.设A,B为n阶方阵,若存在n阶方阵C,使![]() ,则A与B合同。 ( )
,则A与B合同。 ( )
2.若A为正定矩阵,则A的主对角线上的元素皆大于零。
( )
3.若A为负定矩阵,则必有![]() .
( )
.
( )
4.实对称矩阵A半正定当且仅当A的所有顺序主子式全大于或等于零. ( )
5.若A负定,则A的所有顺序主子式全小于零。
( )
6.非退化线性替换把不定二次型变为不定二次型。
( )
7.若实二次型![]() 的符号差为s,令
的符号差为s,令![]() ,则二次型
,则二次型![]() 的符号差为s.
( )
的符号差为s.
( )
8.负定的二次型的矩阵的顺序主子式全小于零。
( )
9. 若矩阵![]() ,
,![]() 正定,则
正定,则![]() 也正定。
( )
也正定。
( )
10. 如果二次型![]() 的各项系数都大于零,则
的各项系数都大于零,则![]() 是正定二次型。
( )
是正定二次型。
( )
三、选择题
1.下列说法错误的是
( )
(A)二次型的标准形不唯一; (B)实二次形的规范形唯一;
(C)二次形必有规范形;
(D)二次型未必满秩。
2.合同于矩阵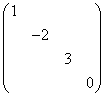 的矩阵是
( )
的矩阵是
( )
(A)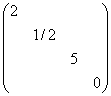 ;
(B)
;
(B)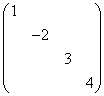 ;
;
(C)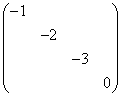 ;
(D)
;
(D)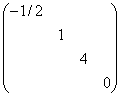 。
。
3.实矩阵A,B合同,则下列不成立的是
( )
(A)|A|,|B|同符号;
(B)A,B有相同的正惯性指数;
(C)A,B有相同的规范形; (D) |A|,|B| 同值。
4.![]() 为
( )
为
( )
(A)正定; (B)半正定; (C)不定; (D)负定。
5.若二次方程![]() 对应的二次型
对应的二次型![]() 正定,那么此二次方程表示的曲线是
(
)
正定,那么此二次方程表示的曲线是
(
)
(A)椭圆; (B)双曲线; (C)抛物线; (D)直线。
6.下列二次型的矩阵对应正定二次型的是
( )
(A) ;(B)
;(B)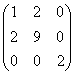 ;(C)
;(C) ;(D)
;(D)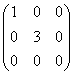 .
.
7.下列二次型的矩阵对应负定二次型的是 (
)
(A)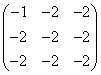 (B)
(B)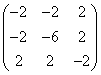 (C)
(C)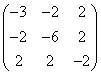 (D)
(D)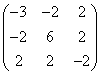
8.下列二次型的矩阵符号差为1的是
( )
(A)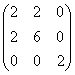 (B)
(B)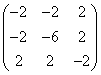 (C)
(C)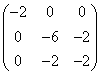 (D)
(D)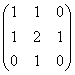
9.关于矩阵的等价与合同,下列说法正确的是
( )
(A)等价的两个矩阵必定合同;
(B)合同的两个矩阵未必等价;
(C)等价的两个矩阵与合同的两个矩阵对应行列式的值都同号;
(D)等价的两个矩阵与合同的两个矩阵秩都相等。
10.下列二次型为半正定的是
( )
(A)![]() ;
;
(B)![]() ;
;
(C)![]() ;
;
(D)![]() .
.
四.计算题
1.求二次型![]() 的标准形,并写出所作的非退化线性替换。
的标准形,并写出所作的非退化线性替换。
2. t取什么值时二次型![]() 为正定二次型。
为正定二次型。
3. 求二次型![]() 的秩与符号差。
的秩与符号差。
4.用配方法化下列二次型为标准形
![]()
5.在复数域中化下列二次型为规范形并写出相应线性变换。
![]()
6.判断二次型![]() 是否正定。
是否正定。
五、证明题
1.证明:若 A 为负定矩阵,则存在可逆矩阵 P,使A+P´P=O.
2.实二次型![]() ,且秩(A)=n. 二次型
,且秩(A)=n. 二次型![]() ,证明:f与g具有相同的符号差,因而有相同的正负惯性指数。
,证明:f与g具有相同的符号差,因而有相同的正负惯性指数。
3. 已知实二次型![]() 是半正定,
是半正定,![]() 为正实数。证明:
为正实数。证明:![]() 是正定的。
是正定的。
4.实对称矩阵![]() 半正定的充分必要条件是存在实方阵
半正定的充分必要条件是存在实方阵![]() 使
使![]() .
.
5. 设实二次型![]() ,证明:
,证明:![]() 的秩等于矩阵
的秩等于矩阵![]() 的秩。
的秩。
6. 证明:二次型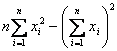 是半正定的。
是半正定的。
7.设![]() 是一个
是一个![]() 阶实对称矩阵,且
阶实对称矩阵,且![]() .证明:必存在实
.证明:必存在实![]() 维向量
维向量![]() 使
使![]() .
.
8.证明:一个实二次型可以分解成两个实系数的一次齐次多项式的乘积的充分必要条件是,它的秩等于2和符号差等于0,或者秩等于1。
9.设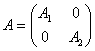 ,
,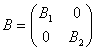 如果
如果![]() 与
与![]() 合同,
合同,![]() 与
与![]() 合同,则
合同,则![]() 与
与![]() 合同。
合同。
10.设![]() ,
,![]() 均为实数,证明:线性方程组
均为实数,证明:线性方程组![]() 必有解。
必有解。
编辑:忠杰
网站:瀚海网:http://hanhai.org
邮箱:nchy_zouzij@163.com
2009.5.20