第四章 矩阵习题
一、
填空题
1.设![]() 为3阶方阵,
为3阶方阵,![]() 注为
注为![]() 的伴随矩阵,有
的伴随矩阵,有![]() ,则
,则![]() .
.
2.设![]() 为4阶方阵,且
为4阶方阵,且![]() ,则
,则![]() ,
, ![]() .
.
3.设![]() 是一个
是一个![]() 矩阵,
矩阵,![]() 是一个
是一个![]() 矩阵,那么
矩阵,那么![]() 是一个 阶矩阵,它的第
是一个 阶矩阵,它的第![]() 行第
行第![]() 列元素为
.
列元素为
.
4.三阶对角矩阵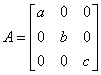 ,则
,则![]() = .
= .
5.设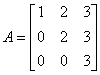 ,则
,则![]() .
.
6.设![]() ,矩阵
,矩阵 的逆矩阵为 。
的逆矩阵为 。
7.设![]() ,则
,则![]() .
.
8.![]() 既是对称矩阵,又是反对称矩阵
既是对称矩阵,又是反对称矩阵![]() ,则
,则![]() 为 矩阵。
为 矩阵。
9.设方阵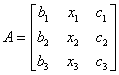 ,
,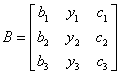 ,且
,且![]() ,则行列式
,则行列式![]() 。
。
10.设![]() 为
为![]() 阶方阵,
阶方阵,![]() 为
为![]() 阶方阵,已知
阶方阵,已知![]() ,则行列式
,则行列式![]() 。
。
二.判断题
1.对于任意![]() 阶矩阵
阶矩阵![]() ,
,![]() ,有
,有![]() .
( )
.
( )
2.如果![]() 则
则![]() .
( )
.
( )
3. 如果![]() ,那么A=O或B=O. ( )
,那么A=O或B=O. ( )
4.如果![]() ,那么|A|=0或|B|=0.
( )
,那么|A|=0或|B|=0.
( )
5.设![]() 都是
都是![]() 阶非零矩阵,且
阶非零矩阵,且![]() ,则
,则![]() 的秩一个等于
的秩一个等于![]() ,一个小于
,一个小于![]() . ( )
. ( )
6.若AB=AC,且|A|≠0,则B=C.
( )
7.若AB=BA,则(AB)n=AnBn.
( )
8.(A+E)(A-E)=(A-E)(A+E).
( )
9.矩阵A、B可逆,则A+B可逆。
( )
10.若矩阵AB可逆,则A,B可逆。
( )
二、
选择题
1.设![]() 是
是![]() 阶对称矩阵,
阶对称矩阵,![]() 是
是![]() 阶反对称矩阵。则下列矩阵中为反对称矩阵的是 ( )
阶反对称矩阵。则下列矩阵中为反对称矩阵的是 ( )
(A) ![]() ; (B)
; (B) ![]() ; (C)
; (C) ![]() ; (D)
; (D) ![]()
2. 设![]() 是一个
是一个![]() 阶矩阵,那么是对称矩阵的是
( )
阶矩阵,那么是对称矩阵的是
( )
(A) ![]() ; (B)
; (B) ![]() ; (C)
; (C) ![]() ; (D)
; (D)![]() .
.
3.以下结论不正确的是
( )
(A)
如果![]() 是上三角矩阵,则
是上三角矩阵,则![]() 也是上三角矩阵;
也是上三角矩阵;
(B)
如果![]() 是对称矩阵,则
是对称矩阵,则![]() 也是对称矩阵;
也是对称矩阵;
(C)
如果![]() 是反对称矩阵,则
是反对称矩阵,则![]() 也是反对称矩阵;
也是反对称矩阵;
(D)
如果![]() 是对角阵,则
是对角阵,则![]() 也是对角阵。
也是对角阵。
4.![]() 是
是![]() 矩阵,
矩阵, ![]() 是
是![]() 矩阵, 若
矩阵, 若![]() 的第
的第![]() 列元素全为零,则
( )
列元素全为零,则
( )
(A) ![]() 的第
的第![]() 行元素全等于零;
(B)
行元素全等于零;
(B) ![]() 的第
的第![]() 列元素全等于零;
列元素全等于零;
(C)![]() 的第
的第![]() 列元素全等于零;
(D)
列元素全等于零;
(D) ![]() 的第
的第![]() 列元素全等于零。
列元素全等于零。
5.设![]() 为
为![]() 阶方阵,则以下命题中正确的是
( )
阶方阵,则以下命题中正确的是
( )
(A) ![]() ; (B)
; (B) ![]() ;
;
(C) ![]() ;
(D)
;
(D) ![]() .
.
6. ![]() 是
是![]() 矩阵,
矩阵,![]() 是
是![]() 矩阵,则
( )
矩阵,则
( )
(A)
当![]() 时,必有行列式
时,必有行列式![]() ;
;
(B)
当![]() 时,必有行列式
时,必有行列式![]() ;
;
(C)
当![]() 时,必有行列式
时,必有行列式![]() ;
;
(D)
当![]() 时,必有行列式
时,必有行列式![]() 。
。
7.以下结论正确的是
( )
(A)
如果矩阵![]() 的行列式
的行列式![]() ,则
,则![]() ;
;
(B)
如果矩阵![]() 、B满足
、B满足![]() ,则
,则![]() 或
或![]() ;
;
(C)
如果矩阵![]() 、B满足
、B满足![]() ,则
,则![]() 或
或![]() ;
;
(D)
如果矩阵![]() 、B满足
、B满足![]() ,则
,则![]() 或
或![]()
8.设![]() 是
是![]() 阶矩阵,
阶矩阵,![]() 适合下列条件中那一条时,
适合下列条件中那一条时, ![]() 是可逆矩阵。
(
)
是可逆矩阵。
(
)
(A)存在某自然数![]() ;
;
(B)存在某自然数![]() ;
;
(C)A主对角线上的元素全为零;
(D)A可逆。
9.![]() 阶方阵
阶方阵![]() 是可逆矩阵的充分必要条件是
(
)
是可逆矩阵的充分必要条件是
(
)
(A)A的行向量组线性无关; (B) A的列向量组线性无关;;
(C)![]() ; (D)
; (D) ![]() .
.
10.![]() 均是
均是![]() 阶矩阵,下列命题正确的是
(
)
阶矩阵,下列命题正确的是
(
)
(A)
若![]() 是可逆矩阵,则从
是可逆矩阵,则从![]() 可推出
可推出![]() ;
;
(B)
若![]() 是可逆矩阵,则必有
是可逆矩阵,则必有![]() ;
;
(C)
若![]() ,则从
,则从![]() 可推出
可推出![]() ;
;
(D)
若![]() ,则必有
,则必有![]() .
.
11.![]() 均
均![]() 阶方阵,若
阶方阵,若![]() ,则有
(
)
,则有
(
)
(A)
![]() ;
(B)
;
(B)![]() ;
;
(C)![]() ;
(D)
;
(D)![]() .
.
12.设![]() 是
是![]() 的伴随阵,则
的伴随阵,则![]() 中位于第i行第j列的元素为
(
)
中位于第i行第j列的元素为
(
)
(A) ![]() ; (B)
; (B) ![]() ; (C)
; (C) ![]() ; (D)
; (D) ![]() .
.
13.设![]() 为方阵,分块对角阵
为方阵,分块对角阵![]() ,则
,则![]() ( )
( )
(A)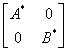 ; (B)
; (B)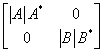 ;
;
(C)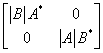 ; (D)
; (D) 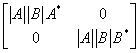 .
.
14.设![]() 是两个
是两个![]() 矩阵,
矩阵,![]() 是
是![]() 阶方阵,那么
(
)
阶方阵,那么
(
)
(A)![]() ; (B)
; (B)![]() ;
;
(C)![]() ;(D)
;(D)![]() .
.
15.对任意一个![]() 阶矩阵
阶矩阵![]() ,若某
,若某![]() 阶矩阵
阶矩阵![]() 能满足
能满足![]() ,那么
,那么![]() 是一个 ( )
是一个 ( )
(A)对称阵; (B)对角阵; (C)单位阵; (D)![]() 的逆矩阵。
的逆矩阵。
16.若矩阵![]() 可逆,则矩阵方程
可逆,则矩阵方程![]() 的解是
的解是![]() ( )
( )
(A)不存在;
(B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() .
.
17. 设![]() 均为
均为![]() 阶非零矩阵,满足
阶非零矩阵,满足![]() ,则
,则![]() 必有
(
)
必有
(
)
(A)![]() ; (B)
; (B)![]() ;
;
(C)![]() ; (D)
; (D)![]() .
.
18.设![]() 是
是![]() 阶方阵,
阶方阵,![]() 为常数,那么
(
)
为常数,那么
(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
19.设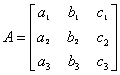 ,若
,若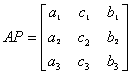 ,则
,则![]() ( )
( )
(A)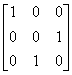 ; (B)
; (B)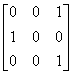 ;(C)
;(C)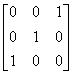 ; (D)
; (D)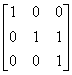 .
.
20.![]() 为n维列向量,A为n阶方阵,则
为n维列向量,A为n阶方阵,则
(1)A(![]() )=(
)=(![]() ;
;
(2)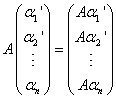 ; (3)(
; (3)(![]() )A=(
)A=(![]() ;
;
(4)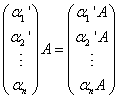 .
.
(A)(1)、(2)正确; (B)(3)、(4)正确;
(C)(2)、(3)正确; (D)(1)、(4)正确。
四.计算题
1.设 ,
, 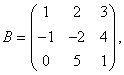 求
求![]()
2.计算下列矩阵的乘积:
(1) 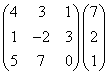 ; (2)
; (2) 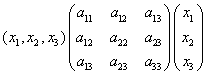 ;
;
(3) 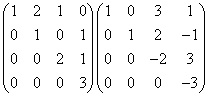 .
.
3.举反例说明下列命题是错误的:
(1)若![]() ,则
,则![]() 或
或![]() ;
;
(2)若![]() ,且
,且![]() ,则
,则![]() .
.
4.设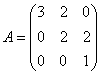 ,求
,求![]() (
(![]() ).
).
5.求下列矩阵的逆矩阵:
(1) 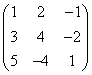 ;
(2)
;
(2) 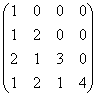 ; (3)
; (3) 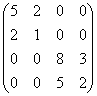 .
.
6.解下列矩阵方程:
(1) 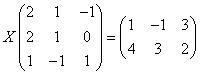 ;
;
(2) ![]() ;
;
(3)设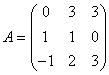 ,
,![]() .
.
7.利用逆矩阵解下列线性方程组: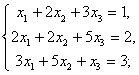
8.设![]() ,其中
,其中![]() ,
,![]() ,求
,求![]() .
.
9.取![]() ,验证
,验证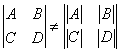 .
.
10.设![]() 阶矩阵
阶矩阵![]() 及
及![]() 阶矩阵
阶矩阵![]() 都可逆,求
都可逆,求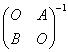 .
.
五.证明题
1.设![]() 为
为![]() 阶矩阵,且
阶矩阵,且![]() 为对称矩阵,证明:
为对称矩阵,证明:![]() 也是对称矩阵.
也是对称矩阵.
2.设![]() 都是
都是![]() 阶对称矩阵,证明
阶对称矩阵,证明![]() 是对称矩阵的充分必要条件是
是对称矩阵的充分必要条件是![]() .
.
3.设![]() (
(![]() 为正整数),证明:
为正整数),证明:![]() .
.
4.设方阵![]() 满足
满足![]() ,证明:
,证明:![]() 及
及![]() 都可逆,并求
都可逆,并求![]() 及
及![]() .
.
5.设A=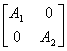 ,其中r(A1)=r1,r(A2)=r2,证明r(A)=r1+r2
,其中r(A1)=r1,r(A2)=r2,证明r(A)=r1+r2
6.设A,B为n阶矩阵,证明矩阵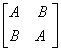 可逆的充分必要条件是矩阵A+B,A-B均可逆。
可逆的充分必要条件是矩阵A+B,A-B均可逆。
7.证明:秩为r的矩阵总可表为r个秩为1的矩阵之和。
8.设A为![]() 矩阵,证明存在非零的n×s矩阵B,使AB=O的充要条件是r(A)<n.
矩阵,证明存在非零的n×s矩阵B,使AB=O的充要条件是r(A)<n.
9. 设A为![]() 阶非奇异阵,
阶非奇异阵,![]() 是两个
是两个![]() 维列向量,证明:
维列向量,证明:
(1) ![]() ;
;
(2) ![]() 可逆当且仅当
可逆当且仅当![]() .
.
10. ![]() 矩阵
矩阵![]() 的秩为
的秩为![]() ,证明:存在
,证明:存在![]() 列满秩矩阵
列满秩矩阵![]() 和
和![]() 行满秩矩阵
行满秩矩阵![]() ,使
,使![]()
11. 设A是一个![]() 阶方阵,
阶方阵,![]() 。证明:A可以表成
。证明:A可以表成![]() 这一类初等矩阵的乘积。
这一类初等矩阵的乘积。
12.![]() 是
是![]() 个
个![]() 维列向量,且
维列向量,且![]() 是可逆的
是可逆的![]() 阶矩阵。证明:当
阶矩阵。证明:当![]() 线性相关时,
线性相关时,![]() 也线性相关;当
也线性相关;当![]() 线性无关时,
线性无关时,![]() 也线性无关。
也线性无关。
13.设![]() 是
是![]() 阶方阵,若存在
阶方阵,若存在![]() 维列向量
维列向量![]() 和正整数k,使得
和正整数k,使得![]() ,证明:向量组
,证明:向量组![]() 线性无关。
线性无关。
14. 设A,B是两个n 阶方阵,证明:![]() 同解。
同解。
15.已知矩阵A,B,A+B均可逆,证明:![]() 可逆并求其逆。
可逆并求其逆。
16.设![]() 。证明:
。证明:![]() 与
与![]() 有相同的线性相关性。
有相同的线性相关性。
注:这里“E”均表示单位矩阵,“O”均表示零矩阵。“![]() ”如无特别说明,均表示A的伴随矩阵。
”如无特别说明,均表示A的伴随矩阵。
编辑:忠杰
网站:瀚海网:http://hanhai.org
邮箱:nchy_zouzij@163.com
2009.5.20