第三章 线性方程组习题
提高题
一.填空、计算题
1. (大连理工大学2005年考研)设向量组![]() 线性无关,
线性无关,
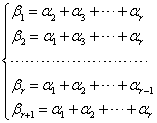
则![]() 线性___关。
线性___关。
2.(兰州大学2004年考研)设A为3级矩阵,![]() 是
是![]() 的三个线性无关的解向量,则
的三个线性无关的解向量,则![]() 的通解为
。
的通解为
。
3. (武汉理工大学2001年考研)设方程组
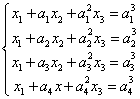
设![]() ,且已知
,且已知![]() 是方程组的两个解,试写出方程组的通解。
是方程组的两个解,试写出方程组的通解。
4. 解方程组
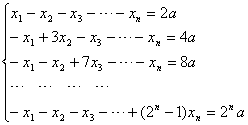
5.(南开大学2005年考研)设齐次线性方程组
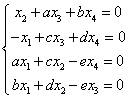
的一般解以![]() 为自由未知量
为自由未知量
(1)求![]() 满足的条件;
满足的条件;
(2)求其基础解系。
三.证明题
1.(温州大学2007年考研)设A,B是n阶方阵,![]() 分别有k,m个线性无关的解向量。(1)证明
分别有k,m个线性无关的解向量。(1)证明![]() 至少有max(k,m)个线性无关的解向量,(2)若k+m>n,证明(A+B)X=O必有非零解。(3)如果
至少有max(k,m)个线性无关的解向量,(2)若k+m>n,证明(A+B)X=O必有非零解。(3)如果![]() 无公共的非零解向量,且k+m=n,则Pn中任一向量均可以表示成
无公共的非零解向量,且k+m=n,则Pn中任一向量均可以表示成![]() 的形式,其中
的形式,其中![]() 分别是
分别是![]() 的解向量。
的解向量。
2.(温州大学2007年考研)![]() 是线性无关向量组,
是线性无关向量组,![]() 为任意向量,证明:要么
为任意向量,证明:要么![]() 线性无关,要么
线性无关,要么![]() 线性无关。
线性无关。
3.(武汉理工大学2001年考研)证明计算题1的方程组中,若![]() 互不相等,则方程组无解。
互不相等,则方程组无解。
4.(大连理工大学2007年考研)设方程组为
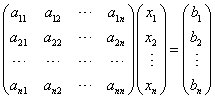
如果 ,则方程组有解。
,则方程组有解。
5.(东南大学2002年考研)设![]() 线性无关,则
线性无关,则
![]()
的秩为3.
6.(大连理工大学2005年考研)设![]() 为
为![]() 级方阵,且秩
级方阵,且秩![]() 秩
秩![]() ,证明:对任意自然数
,证明:对任意自然数![]() ,有秩
,有秩![]() =秩
=秩![]() .
.
编辑:忠杰
网站:瀚海网:http://hanhai.org
邮箱:nchy_zouzij@163.com
2009.5.20