第三章 线性方程组习题
基本题
一.
填空题
1. 若向量组![]() 线性无关,则向量组
线性无关,则向量组![]() 线性___关。
线性___关。
2. ![]() 个
个![]() 维向量组成的向量组为线性____关向量组。
维向量组成的向量组为线性____关向量组。
3.设向量组![]() 线性无关,则常数
线性无关,则常数![]() 满足___________时,向量组
满足___________时,向量组![]() 线性无关。
线性无关。
4. 设秩(A) = ![]() , 秩(B) =
, 秩(B) = ![]() ,则秩
,则秩![]() ___________,秩
___________,秩![]() ___________.
___________.
5. 设矩阵A中有一个r阶子式不为0,则r(A)
, 设矩阵A中所有的r+1阶子式全为0,则r(A)
.
6. 矩阵A的一个最高阶非零子式对应的行向量组为A的行向量组的
。
7.非齐次线性方程组![]() 注(
注(![]() 为
为![]() 矩阵)有唯一解的的充分必要条件是____________。
矩阵)有唯一解的的充分必要条件是____________。
8.已知4元非齐次线性方程组的系数阵为A![]() ,
,![]() 是它的三个解向量,其中
是它的三个解向量,其中![]() ,则此线性方程组通解的形式为_______________。
,则此线性方程组通解的形式为_______________。
9. 设![]() 阶方阵
阶方阵![]() 的各行元素之和均为零,且
的各行元素之和均为零,且![]() ,则线性方程组
,则线性方程组![]() 的通解为________。
的通解为________。
10. 在线性方程组AX=B有解的条件下,解是唯一的充分必要条件是AX=0
。
二.判断题
1.若![]() =0时,
=0时,![]() ,则向量组
,则向量组![]() 线性无关。 ( )
线性无关。 ( )
2.若向量组![]() 与
与![]() 均线性无关,则
均线性无关,则![]() ,
,![]() 线性无关。
( )
线性无关。
( )
3.方程个数小于未知量个数的线性方程组必有无穷多解。 ( )
4.同秩的两个向量组未必等价。 ( )
5.向量组中某向量能被其余向量表示,则去掉它不影响它的秩。 ( )
6.向量组中某向量不能被其余向量表示,则去掉它后向量组的秩必改变。 ( )
7.3个未知量,5个方程组成的方程组中,必有一个方程能被其余的方程线性表示。 ( )
8.不同秩的两个向量组必不等价。 ( )
9.向量组的向量各加一个分量,其秩不变。 ( )
10.方程组中自由未知量是唯一确定的。 ( )
三、选择题
1.已知向量组![]() 线性相关,则下列命题成立的是
( )
线性相关,则下列命题成立的是
( )
(A)![]() 中至少有一个零向量;
中至少有一个零向量;
(B)对任意一组不全为零的常数![]() ,有
,有![]() ;
;
(C)![]() 中任意一个向量均可由其余
中任意一个向量均可由其余![]() 个向量线性表示;
个向量线性表示;
(D)秩(![]() )<
)< ![]() .
.
2.对于齐次线性方程组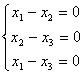 ,它的一个基础解系是
( )
,它的一个基础解系是
( )
(A)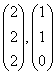 ; (B)
; (B) 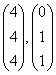 ; (C)
; (C)![]() ; (D)
; (D)![]() .
.
3.当![]() 取下列何值时,方程组
取下列何值时,方程组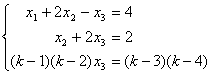 无解。
( )
无解。
( )
(A)2; (B)3; (C) 4; (D)5.
4.设向量组![]() 是齐次线性方程组
是齐次线性方程组![]() 的一个基础解系,则也是
的一个基础解系,则也是![]() 的一个基础解系的向量组是
( )
的一个基础解系的向量组是
( )
(A) ![]() ; (B)
; (B) ![]() ;
;
(C)![]() ;
(D)
;
(D)![]() .
.
5.
![]() 为
为![]() 矩阵,秩(A) =
矩阵,秩(A) = ![]() ,下列结论正确的是 ( )
,下列结论正确的是 ( )
(A)齐次线性方程组![]() 只有零解; (B)非齐次线性方程组
只有零解; (B)非齐次线性方程组![]() 有无穷多解;
(C) A中任一个
有无穷多解;
(C) A中任一个![]() 阶子式均不等于零;
(D)A中任意
阶子式均不等于零;
(D)A中任意![]() 个列向量必线性无关。
个列向量必线性无关。
6. ![]() 是齐次线性方程组
是齐次线性方程组![]() 的一个基础解系,则该方程组的一个基础解系是
( )
的一个基础解系,则该方程组的一个基础解系是
( )
(A)可由![]() 线性表示的向量组;(B)与
线性表示的向量组;(B)与![]() 等秩的向量组 ;
等秩的向量组 ;
(C) ![]() ;
(D)
;
(D)![]() .
.
7. 设![]() , 两个
, 两个![]() 维向量组
维向量组![]() (1) 和
(1) 和![]() (2), 下述正确的是( )
(2), 下述正确的是( )
(A)若(1)可由(2)线性表出, 则(1)线性相关;
(B)若(1)可由(2)线性表出, 则(1)未必线性相关;
(C)若(1)可由(2)线性表出, 则当(2)线性无关时, (1)线性无关;
(D)若(1)可由(2)线性表出, 则仅当(2)线性相关时, (1)线性相关.
8. 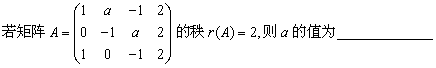
![]()
9. 设向量组![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,
,![]() =
=![]() ,则极大无关组为( )。
,则极大无关组为( )。
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10. 设线性方程组AX=B的一般解为![]() (x3是自由未知量),则( )
(x3是自由未知量),则( )
(A)只有令x3=0才能求出AX=B的特解; (B)令x3=1求得特解为![]() ;
;
(C)令x3=2求得特解为![]() ;
(D)令x3=0求得特解为
;
(D)令x3=0求得特解为![]() .
.
四.
计算题
1.求向量组![]() 的秩,并求其中一个极大线性无关组。
的秩,并求其中一个极大线性无关组。
2.设有向量![]() ,问
,问![]() 为何值时:
为何值时:
(1)![]() 可由
可由![]() 线性表示,且表达式唯一;
线性表示,且表达式唯一;
(2)![]() 可由
可由![]() 线性表示,且表达式不唯一;
线性表示,且表达式不唯一;
(3)![]() 不可由
不可由![]() 线性表示。
线性表示。
3.对于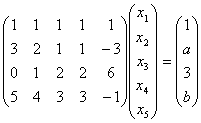 ,
,
(1)![]() 为何值时,方程组有解;
为何值时,方程组有解;
(2)方程组有解时,求导出组的一个基础解系;
(3)方程组有解时,求其通解。
4.已知齐次线性方程组(I)为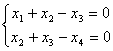 ,齐次线性方程组(Ⅱ)的一个基础解系为
,齐次线性方程组(Ⅱ)的一个基础解系为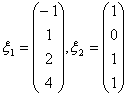 .求(I),(Ⅱ)的所有公共解,并指明该公共解如何由(I),(Ⅱ)的基础解系线性表示。
.求(I),(Ⅱ)的所有公共解,并指明该公共解如何由(I),(Ⅱ)的基础解系线性表示。
5.![]() 满足什么条件时,方程组
满足什么条件时,方程组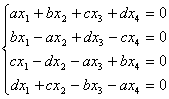 只有零解?
只有零解?
6.求解下列非齐次线性方程组:
(1)  (2)
(2) 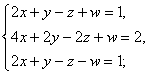
7.求解下列齐次线性方程组:
(1) 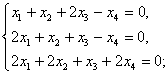 (2)
(2) 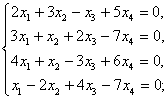
8.非齐次线性方程组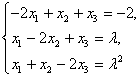 。当
。当![]() 取何值时有解?并求出它的解.
取何值时有解?并求出它的解.
9.判断下列两对向量组是否等价
(1)![]() 与
与![]()
(2).![]() 与
与![]()
![]() .
.
10.求下列矩阵的秩,并分别求其最高阶非零子式:
(1) 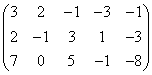 (2)
(2) 
五.证明题
1.设向量组![]() 线性无关,且
线性无关,且![]() ,证明:
,证明:![]() 也线性无关。
也线性无关。
2.已知向量组A: ;B:
;B: .证明:B组能由A组线性表示,但A组不能由B组线性表示。
.证明:B组能由A组线性表示,但A组不能由B组线性表示。
3.已知向量组![]() 线性无关,向量组
线性无关,向量组![]() 线性相关。证明:
线性相关。证明:![]() 能唯一由
能唯一由![]() 线性表示。
线性表示。
4.设![]() 为一个向量组,
为一个向量组,![]() ,证明:向量组
,证明:向量组![]() 线性相关。
线性相关。
5.设![]() 是某非齐次线性方程组的一个解。
是某非齐次线性方程组的一个解。![]() 为其导出组的一个基础解系,证明:(1)
为其导出组的一个基础解系,证明:(1)![]() 线性无关;
线性无关;
(2)若![]() 为另一特解,则
为另一特解,则![]() 线性相关。
线性相关。
6. 设齐次线性方程组
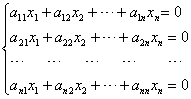 的系数行列式D=0,而D中某一元素aij的代数余子式Aij≠0,证明:这个方程组的每一解都可写成(kAi1,kAi2,…,kAin)的形式。
的系数行列式D=0,而D中某一元素aij的代数余子式Aij≠0,证明:这个方程组的每一解都可写成(kAi1,kAi2,…,kAin)的形式。
7. 设n阶行列式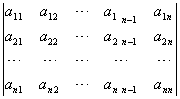 ≠0,证明线性方程组
≠0,证明线性方程组
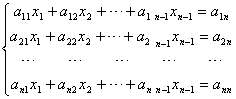
无解。
8. 设![]() 为
为![]() 维向量组,证明:此向量组线性无关当且仅当任一个由此向量组线性表出的向量的表示法是唯一的.
维向量组,证明:此向量组线性无关当且仅当任一个由此向量组线性表出的向量的表示法是唯一的.
9. 已知![]() 线性无关,
线性无关, ![]() 为两个向量,若
为两个向量,若![]() 线性相关,
线性相关,![]() 线性无关,证明:
线性无关,证明:![]() 必线性无关(
必线性无关(![]() 为任意常数).
为任意常数).
10.证明:与基础解系个数相同且等价的向量组是仍是方程组的一个基础解系。
注:为了方便表示,线性方程组
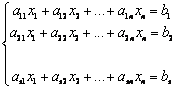
表示为矩阵方程:AX=B的形式。其中![]() 为系数阵。X为未知量对应向量;B为常数项对应向量。若是齐次方程,则B改为O。具体意义见下一章,现在只当做形式。
为系数阵。X为未知量对应向量;B为常数项对应向量。若是齐次方程,则B改为O。具体意义见下一章,现在只当做形式。
编辑:忠杰
网站:瀚海网:http://hanhai.org
邮箱:nchy_zouzij@163.com
2009.5.20