第七章  线性变换习题

提高题

一．填空、计算题

 1.（上海师大2005考研）设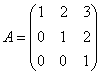，用你的方法求矩阵P，使得.

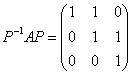2.（南开大学2003考研）设V为3维线性空间，V上的线性变换在V的一组基下的矩阵为 

                 

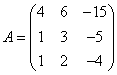
问：f可否在V的某组基下的矩阵为

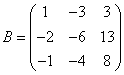
为什么？

3.（孝感人民大学2004年考研）设P[x]3表示实数域上次数小于3的多项式，加上零多项式构成的线性空间，而 是P[x]3的一组基。线性变换A满足

（1）求在已知基下的矩阵；

（2）设，求Af(x).

4.(南京理工大学2005年考研)在数域P上的n阶方阵的全体中，求出所有仅与自己相似的矩阵。

5. （中山大学2005考研）由三个函数1，cos t, sin t构成线性空间V，求线性变换T:VV,f(t)f(t+)的特征多项式。

 

二．证明题

1. （复旦大学2000年考研）设为一个阶方阵且的秩等于的秩。证明的秩等于的秩。（提示：利用若当标准型）

2. （大连理工2005年考研） 设A是数域上的维线性空间的一个线性变换,是A的最小多项式,在中,,、均为首项系数为1的多项式,且与互素,令

(A)(),   (A)().

证明:

(1)  和都是A的不变子空间；

(2) ；

(3)  A的最小多项式是, A的最小多项式是.

3.（上海交大2003年考研）A，B都是正定矩阵，证明AB的特征值是实数。

4.（浙江大学2004年考研）设A是n阶复矩阵，若存在证整数m，使得（这里E为单位矩阵），则A与对角阵相似。

5.（上海交大2003年考研）记V=，P为数域。假设AV有特征值。   但 均不是A的特征值。试证明：V的变换是同构。

6.（南开大学2004年考研）在实n维线性空间R是否存在线性变换A，满足：

                    

证明你的结论。

7.（兰州大学2004年考研）设A是正定矩阵，B是n级半正定矩阵，且满足，证明B是正定矩阵，且A与B相似。

                                                    编辑：忠杰

                                                    网站：瀚海网：http://hanhai.org

                                                    邮箱：nchy_zouzij@163.com

                                                                   2009．5．20