第七章 线性变换习题
基本题
一、填空题
1.设![]() 是线性空间
是线性空间![]() 的一组基,
的一组基,![]() 的一个线性变换
的一个线性变换![]() 在这组基下的矩阵是
在这组基下的矩阵是![]() 则
则![]() 在基
在基![]() 下的矩阵
下的矩阵![]() =_________,而可逆矩阵T=_________满足
=_________,而可逆矩阵T=_________满足![]()
![]() 在基
在基![]() 下的坐标为_________.
下的坐标为_________.
2.设![]() 为数域
为数域![]() 上秩为
上秩为![]() 的
的![]() 阶矩阵,定义
阶矩阵,定义![]() 维列向量空间
维列向量空间![]() 的线性变换
的线性变换![]() :
: ![]() ,则
,则![]() =_______,维
=_______,维![]() =______,维
=______,维![]() =_____.
=_____.
3.设![]() 是
是![]() 维线性空间
维线性空间![]() 的线性变换,且
的线性变换,且![]() 在任一基下的矩阵都相同,则
在任一基下的矩阵都相同,则![]() 为________变换。
为________变换。
4.设![]() 阶矩阵
阶矩阵![]() 的全体特征值为
的全体特征值为![]() ,
,![]() 为任一多项式,则
为任一多项式,则![]() 的全体特征值为________.
的全体特征值为________.
5.若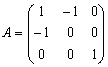 与
与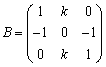 相似,则
相似,则![]() =
.
=
.
6.![]() :
:![]() ,
,![]() ;
;![]() :
:![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
7.设三阶方阵A的特征多项式为![]() ,则
,则![]() .
.
8.设![]() 是向量空间V的一个基,线性变换s在此基下对应的矩阵为
是向量空间V的一个基,线性变换s在此基下对应的矩阵为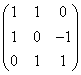 ,则s在基
,则s在基![]() 下对应的矩阵为
.
下对应的矩阵为
.
9.设实二次型![]() ,
,![]() ,其中二次型的矩阵
,其中二次型的矩阵![]() 的特征值之和为1,特征值之积为
的特征值之和为1,特征值之积为![]() .则
.则![]() ,
, ![]() .
.
10. 设F n={(x1, x 2,…, x n)| x iÎF}是数域F上的n维空间,定义线性变换![]() :
:
![]() ( x1, x 2,…, x n)=(0, x 1,…, x n);
( x1, x 2,…, x n)=(0, x 1,…, x n);
则 ![]() 的维数是
。
的维数是
。
11.设实二次型![]() ,
,![]() ,其中二次型的矩阵
,其中二次型的矩阵![]() 的特征值之和为1,特征值之积为-12.则
的特征值之和为1,特征值之积为-12.则![]() ,
, ![]() .
.
12.![]() 满足
满足![]() ,则
,则![]() 有特征值___________。
有特征值___________。
二、判断题
1.设![]() 是
是![]() 维向量空间
维向量空间![]() 的两个线性变换,
的两个线性变换,![]() 分别是
分别是![]() 关于
关于![]() 的基
的基![]() 的矩阵,则当
的矩阵,则当![]() 时,必有:
时,必有:![]() .
( )
.
( )
2.设![]() 为
为![]() 维线性空间
维线性空间![]() 的一个线性变换,则由
的一个线性变换,则由![]() 的秩+
的秩+![]() 的零度=
的零度=![]() ,有
,有![]() ( )
( )
3.在线性空间![]() 中定义变换
中定义变换![]() :
:![]() ,则
,则![]() 是
是![]() 的一个线性变换。 ( )
的一个线性变换。 ( )
4.若![]() 为
为![]() 维线性空间
维线性空间![]() 的一个线性变换,则
的一个线性变换,则![]() 是可逆的当且仅当
是可逆的当且仅当![]() ={0}. ( )
={0}. ( )
5.设![]() 为线性空间
为线性空间![]() 的一个线性变换,
的一个线性变换,![]() 为
为![]() 的一个子集,若
的一个子集,若![]() 是
是![]() 的一个子空间,则
的一个子空间,则![]() 必为
必为![]() 的子空间。
( )
的子空间。
( )
6.![]() 阶方阵A至少有一个特征值为零的充分必要条件是
阶方阵A至少有一个特征值为零的充分必要条件是![]() .
( )
.
( )
7.已知![]() ,其中
,其中![]() 为
为![]() 阶可逆矩阵,
阶可逆矩阵,![]() 为一个对角矩阵.则A的特征向量与P有关。
( )
为一个对角矩阵.则A的特征向量与P有关。
( )
8.数域P上的n维线性空间V的线性变换的全体构成的线性空间是n2维的 ( )
9.若![]() ,且
,且![]() 为A-子空间,则
为A-子空间,则![]() 也为A-子空间。
( )
也为A-子空间。
( )
10.若![]() 上的线性空间V上的线性变换A的特征多项式可以在
上的线性空间V上的线性变换A的特征多项式可以在![]() 上完全分解,则它一定存在一组基,在此基下的矩阵为若尔当标准型。
( )
上完全分解,则它一定存在一组基,在此基下的矩阵为若尔当标准型。
( )
三.选择题
1. 若A,B 均为n阶方阵,A,B有相同的特征值且均非零,则: ( )
(A)A,B相似;(B)A,B合同; (C)A,B等价; (D)A,B有相同的若尔当标准型。
2.若矩阵P与Q相似,下列说法错误的是: ( )
(A)P与Q有相同的特征值;
(B)P与Q有相同的对角形;
(C)P 与Q可以看作同一线性变换在不同基下的矩阵;
(D)P与 Q对应的行列式的值相同。
3.设W是n维线性空间V的一个A-子空间,![]() ,下面说法不正确的是
( )
,下面说法不正确的是
( )
(A)W可能是真子空间; B) T也是A-子空间;
(C) A限制在 W 上也是线性变换; (D) A的秩为n,那么T也是A-子空间。
4. 设矩阵A=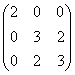 与 D=
与 D=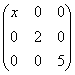 相似,则x=
( )
相似,则x=
( )
(A)1; (B) -1; (C)2; (D)不能确定。
5.设![]() 是
是![]() 维线性空间
维线性空间![]() 的线性变换,那么下列说法错误的是
( )
的线性变换,那么下列说法错误的是
( )
(A)![]() 是单射
是单射![]()
![]() ={0}; (B)
={0}; (B)![]() 是满射
是满射![]()
![]() 的秩=
的秩=![]() ;
;
(C)![]() 是可逆的
是可逆的![]()
![]() =
=![]() ; (D)
; (D)![]() 是双射
是双射![]()
![]() 是单位变换。
是单位变换。
6.Q为n阶方阵,其秩为r.A![]() 为一个
为一个![]() 上的线性变换(
上的线性变换(![]() ).A的核的维数为
( )
).A的核的维数为
( )
(A)r维; (B) n维; (C) n-r维; (D)0维。
7.设A是n阶对称矩阵,P是n阶可逆矩阵,已知n维列向量a是A的属于特征值l的特征向量,则矩阵(P-1AP)![]() 属于特征值l的特征向量是
( )
属于特征值l的特征向量是
( )
(A)P-1a;
(B)P![]() a;
(C)Pa;
(D)(P-1)
a;
(C)Pa;
(D)(P-1)![]() a.
a.
8.设s,t 是V的线性变换,i 是恒等变换,则下列结论中不一定正确的是 ( )
(A)(s+i)![]() 是 s-i 的不变子空间;
(B)(s+t)
是 s-i 的不变子空间;
(B)(s+t)![]() 是 s+t 的不变子空间;
是 s+t 的不变子空间;
(C)t![]() 是 s 的不变子空间;
(D)(t-i)V 是
t+i 的不变子空间.
是 s 的不变子空间;
(D)(t-i)V 是
t+i 的不变子空间.
9.令![]() 是
是![]() 的任意向量,则是
的任意向量,则是![]() 的线性变换的映射是
( )
的线性变换的映射是
( )
(A)![]() ;
(B)
;
(B)![]() ;
;
(C)![]() ;
(D)
;
(D)![]() .
.
10.关于线性空间V上的线性变换A的值域与核,下列说法正确的是
( )
(A)AV的基与A -1(0)的基合并可成为V的基;
(B) AV的基的原象为V的基;
(C) AV中线性无关的向量组的原象仍线性无关;
(D)AV中线性相关的向量组的原象仍线性相关。
四、计算题
1.判断矩阵![]() 是否可对角化?若可对角化,求一个可逆矩阵T,使成对角形。
是否可对角化?若可对角化,求一个可逆矩阵T,使成对角形。
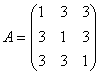
2.在线性空间![]() 中定义变换
中定义变换![]() :
:![]()
(1)证明:![]() 是
是![]() 的线性变换. (2)求
的线性变换. (2)求![]() 与
与![]()
3.设![]() 是
是![]() 的线性变换,
的线性变换,![]()
(1)求![]() 的一个基和维数; (2)求
的一个基和维数; (2)求![]() 的一个基和维数.
的一个基和维数.
4.设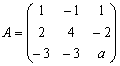 与
与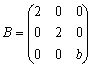 相似。
相似。
(1)求![]() 的值; (2)求可逆矩阵P,使
的值; (2)求可逆矩阵P,使![]() .
.
5. 设F3[x] 表示一切次数不大于3的数域F上的多项式连同零多项式所成的向量空间,D是微分变换。(1)求D的所有特征根;(2)求F3[x]一组基,使得微分变换D在此基下的矩阵为 B= 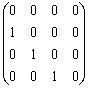 .03gd
.03gd
6.设四维线性空间![]() 上的线性变换A在一组基
上的线性变换A在一组基![]() 下的矩阵为
下的矩阵为  .
.
(1)求出A![]() 的维数,并求出A
的维数,并求出A![]() 的一组基;(2)求出A
的一组基;(2)求出A![]() 的维数,并求出A
的维数,并求出A![]() 的一组基。
的一组基。
7.![]() 中线性变换
中线性变换![]() ,求
,求![]() 在基
在基![]() 下的矩阵。
下的矩阵。
8.设![]() 是3维线性空间V的一组基, 线性变换A在这组基下的矩阵为
是3维线性空间V的一组基, 线性变换A在这组基下的矩阵为
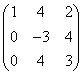
(1)求A在基![]()
![]()
![]() 下的矩阵;
下的矩阵;
(2)求A的特征值与特征向量。(06年补考)
9.设已知线性空间V=![]() (数域P上的二阶方阵全体.加法定义为矩阵的加法;数乘为矩阵的数乘)
(数域P上的二阶方阵全体.加法定义为矩阵的加法;数乘为矩阵的数乘)
![]()
判断:(1)V1是否为V的子空间?其基与维数?
(2)若在V中定义变换:
![]()
![]()
A是否为V的线性变换?
(3)V1是否为![]() -子空间,说明理由。(2007年试卷a)
-子空间,说明理由。(2007年试卷a)
10.在![]() 中定义线性变换:
中定义线性变换:
1)![]()
2)![]()
分别求![]() ,
,![]() 在基
在基![]() 下的矩阵。
下的矩阵。
11.设A= ,求 A100
,求 A100
12.设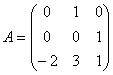
(1)若把![]() 看成有理数域上的矩阵,判断
看成有理数域上的矩阵,判断![]() 是否可对角化,写出理由;
是否可对角化,写出理由;
(2)若把![]() 看成复数域上的矩阵,判断
看成复数域上的矩阵,判断![]() 是否可对角化,写出理由。
是否可对角化,写出理由。
五.证明题
1.若![]() 是一个
是一个![]() 阶矩阵,且
阶矩阵,且![]() ,则
,则![]() 的特征值只能是0和1.
的特征值只能是0和1.
2.若A为线性空间V的线性变换,则(1)A 为幂零的线性变换当且仅当A 的特征多项式的根全为零。 (2)A 可对角化,则![]() .
.
3. 若数域P上的n维向量空间V的线性变换A满足![]() ,则称之为对合变换, 证明
,则称之为对合变换, 证明
(1) A的特征值为![]()
(2)![]() (
(![]() 为属于1的特征子空间,
为属于1的特征子空间,![]() 为属于-1的子空间)
为属于-1的子空间)
4.设V是数域P上的一个有限维向量空间.证明,对于V的线性变换![]() 来说,下列三个条件是等价的:(1)
来说,下列三个条件是等价的:(1)![]() 是满射; (2)
是满射; (2)![]() = {0}; (3)
= {0}; (3) ![]() 非奇异。
非奇异。
5.令V是复数域上的一个n维向量空间,![]() ,
,![]() 是V的线性变换,且
是V的线性变换,且![]() .
.
(1)证明,![]() 的每一特征子空间都在
的每一特征子空间都在![]() 之下不变;(2)
之下不变;(2) ![]() 与
与![]() 在V中有一公共特征向量.
在V中有一公共特征向量.
6.设A,B是复数域上n阶矩阵。证明,AB与BA有相同的特征根,并且对应的特征根的重数也相同。
7.设![]() 是向量空间V上的线性变换,证明:
是向量空间V上的线性变换,证明:![]() 不可逆的充分必要条件是
不可逆的充分必要条件是![]() 以零作为一个特征值。
以零作为一个特征值。
8.规定:
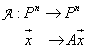
其中A为一个固定的矩阵。证明:(1)A为![]() 的线性变换,找一组基,使得在此基下的矩阵为A.(2)若A可逆,则A可以作为
的线性变换,找一组基,使得在此基下的矩阵为A.(2)若A可逆,则A可以作为![]() 上的自同构。
上的自同构。
编辑:忠杰
网站:瀚海网:http://hanhai.org
邮箱:nchy_zouzij@163.com
2009.5.20