第九章 欧几里得空间习题

提高题

一．填空、计算题

1. （大连理工大学2005年考研） 正交矩阵的实特征值为___________.

2. 已知A=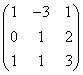 求上三角阵S与正交阵U，使得AS=U.

3.（南开大学2004年考研）给定^2注标准度量，求²中保持以以下点作为端点的正方形

A=(1,1)，B=(-1,1)，C=(-1,-1)，D=(1,-1)

整体不变（即正方形四条边上的点经过线性变换后仍落在四条边上）的正交变换。

4.（华南理工大学2007考研）设线性方程组

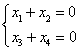
的解空间为W.求向量（2，3，4，5）到空间W的内射影以及到W的距离。

5.（东南大学2004年考研）设为欧氏空间的一组标准正交基， 求正交变换H，使得.

二．证明题

1. （复旦大学2000年考研）设为一个阶正交阵，为一组线性无关的列向量，对于都有.如果的行列式等于1，证明是单位矩阵。

2.（大连理工大学2005年考研） 设是一个维欧氏空间,是的一个标准正交基, A是的一个线性变换,是A关于这个基的矩阵,证明: (A(),), .(其中( , )表示内积)

3. （华中科大2005年考研）证明: 任一阶实可逆矩阵可以分解成一个正交阵与一个正定阵之积, 即.

4.（南开大学2008考研）线性变换T，满足或之一，则T为对称变换或反对称变换。

5.（温州师范学院2006年考研）设A为n级实对称阵，且A的特征值为0或，证明对任意两个奇数l与m，.

6. （南京大学2001年考研）证明:设E是n阶单位矩阵,A是n阶正定矩阵,证明: |E+A|>1.

7. 设是两个实对称矩阵,且B是正定矩阵.证明存在一实可逆矩阵T使

同时为对角形.

8. 证明:奇数维欧氏空间中的旋转一定以1作为它的一个特征值。.

9. （大连理工大学2005年考研）设是一个维欧氏空间,是的一个标准正交基, A是的一个线性变换,是A关于这个基的矩阵,证明: (A(),), .(其中( , )表示内积)。

注：这里“”均表示实数域。

编辑：忠杰

网站：瀚海网：http://hanhai.org

邮箱：nchy_zouzij@163.com

2009．5．20