第九章 欧氏空间习题
基本题
一、填空题
1.设![]() 是一个欧氏空间,
是一个欧氏空间, ![]() ,若对任意
,若对任意![]() ,都有
,都有![]() ,则
,则![]() =_________.
=_________.
2.在![]() 维欧氏空间
维欧氏空间![]() 中,向量
中,向量![]() 在标准正交基
在标准正交基![]() 下的坐标是
下的坐标是![]() ,那么
,那么![]() =_________,
=_________,![]() =_________.
=_________.
3.若![]() 是一个正交矩阵,则方程组
是一个正交矩阵,则方程组
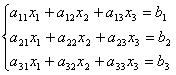
的解为
.
4.已知三维欧式空间![]() 中有一组基
中有一组基![]() ,其度量矩阵为
,其度量矩阵为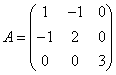 ,则向量
,则向量![]() 的长度为 .
的长度为 .
5.设![]() 注中的内积为
注中的内积为![]() 则在此内积之下的度量矩阵为
.
则在此内积之下的度量矩阵为
.
6.设![]() ,若
,若![]() 与
与![]() 正交,则
正交,则![]() .
.
7.若欧氏空间V在某组基下的度量矩阵为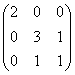 ,某向量在此组基下的坐标为
,某向量在此组基下的坐标为![]() ,则它的长度为 ,在此基下,向量
,则它的长度为 ,在此基下,向量![]() 与向量
与向量![]() 的夹角为 .
的夹角为 .
8.在欧氏空间中,若![]() 线性相关,且
线性相关,且![]() ,则
,则![]() .
.
9.![]()
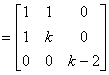 是度量阵,则
是度量阵,则![]() 必须满足条件______________.
必须满足条件______________.
10.线性空间在不同基下的过渡阵、线性变换在某组基下的矩阵、欧氏空间的度量阵这三类矩阵中,可以为退化阵的是 .
二、判断题
1.在实线性空间![]() 中,对向量
中,对向量![]() ,定义
,定义![]()
![]()
![]() ,那么
,那么![]() 构成欧氏空间。
( )
构成欧氏空间。
( )
2.在实线性空间![]() 中,对于向量
中,对于向量![]() ,定义
,定义![]() ,则
,则![]() 构成欧氏空间。
( )
构成欧氏空间。
( )
3.![]() 是欧氏空间
是欧氏空间![]() 的一组基,对于
的一组基,对于![]() 中任意向量
中任意向量![]() ,均有
,均有![]() (
(![]() 分别是在此基下的坐标),则此基必为标准正交基。
( )
分别是在此基下的坐标),则此基必为标准正交基。
( )
4.欧氏空间![]() 中的线性变换可以将椭圆映射成圆。
( )
中的线性变换可以将椭圆映射成圆。
( )
5.V与W均欧氏空间且同构,则它们作为线性空间也必同构。
( )
6.设![]() 是一个欧氏空间,
是一个欧氏空间,![]() ,并且
,并且![]() ,则
,则![]() 与
与![]() 正交。 ( )
正交。 ( )
7.设![]() 是一个欧氏空间,
是一个欧氏空间,![]() ,并且
,并且![]() ,则
,则![]() 线性无关。
( )
线性无关。
( )
8.若![]() 都是欧氏空间
都是欧氏空间![]() 的对称变换,则
的对称变换,则![]() 也是对称变换。
( )
也是对称变换。
( )
9.欧氏空间![]() 中,
中,![]() 为对称变换。
( )
为对称变换。
( )
10.![]() 是欧氏空间
是欧氏空间![]() 的线性变换,
的线性变换,![]() 中向量
中向量![]() 的夹角为
的夹角为![]() ,而
,而![]() 的夹角为
的夹角为![]() ,则
,则![]() 不是
不是![]() 的正交变换。
( )
的正交变换。
( )
三.选择题
1.关于欧几里得空间,下列说法正确的是 ( )
(A)任一线性空间都能适当定义内积成为欧几里得空间;
(B)欧几里得空间未必是线性空间;
(C)欧几里得空间必为实数域上的线性空间;
(D)欧几里得空间可以为有理数域上的线性空间。
2. 设![]() ,
,![]() 是相互正交的
是相互正交的![]() 维实向量,则下列各式中错误的是
( )
维实向量,则下列各式中错误的是
( )
(A)![]()
![]() .
.![]()
(C)![]() (D)
(D)![]()
3. 对于![]() 阶实对称矩阵
阶实对称矩阵![]() ,以下结论正确的是
( )
,以下结论正确的是
( )
(A)一定有![]() 个不同的特征根;(B)存在正交矩阵
个不同的特征根;(B)存在正交矩阵![]() ,使
,使![]() 成对角形;
成对角形;
(C)它的特征根一定是整数;(D)属于不同特征根的特征向量必线性无关,但不一定正交
4.设![]() 是
是![]() 维欧氏空间
维欧氏空间![]() 的对称变换,则
( )
的对称变换,则
( )
(A)![]() 只有一组
只有一组![]() 个两两正交的特征向量; (B)
个两两正交的特征向量; (B)![]() 的特征向量彼此正交;
的特征向量彼此正交;
(C)![]() 有
有![]() 个两两正交的特征向量;
个两两正交的特征向量;
(D)![]() 有
有![]() 个两两正交的特征向量
个两两正交的特征向量![]() 有
有![]() 个不同的特征根。
个不同的特征根。
5.![]() ,定义:
,定义:![]() ,则满足下列何中情况可使
,则满足下列何中情况可使![]() 作成欧氏空间
( )
作成欧氏空间
( )
(A)![]() ;
(B)
;
(B)![]() 是全不为零的实数;
是全不为零的实数;
(C)![]() 都是大于零的实数; (D)
都是大于零的实数; (D)![]() 全是不小于零的实数
全是不小于零的实数
6.![]()
![]() ,
,![]() 为三阶实方阵,定义
为三阶实方阵,定义![]() ,下列可使定义作为
,下列可使定义作为![]() 的内积的矩阵是
( )
的内积的矩阵是
( )
(A)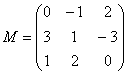 ;
(B)
;
(B)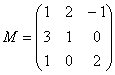 ;
;
(C)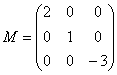 ;
(D)
;
(D)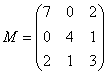 .
.
7.若欧氏空间![]() 的线性变换
的线性变换![]() 关于
关于![]() 的一个标准正交基的矩阵为
的一个标准正交基的矩阵为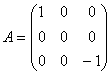 ,则下列正确的是
( )
,则下列正确的是
( )
(A)![]() 是对称变换; (B)
是对称变换; (B)![]() 是对称变换且是正交变换;
是对称变换且是正交变换;
(C)![]() 不是对称变换; (D)
不是对称变换; (D)![]() 是正交变换。
是正交变换。
8.若![]() 是
是![]() 维欧氏空间
维欧氏空间![]() 的一个对称变换,则下列成立的选项是
( )
的一个对称变换,则下列成立的选项是
( )
(A)![]() 关于
关于![]() 的仅一个标准正交基的矩阵是对称矩阵;
的仅一个标准正交基的矩阵是对称矩阵;
(B)![]() 关于
关于![]() 的任意基的矩阵都是对称矩阵;
的任意基的矩阵都是对称矩阵;
(C)![]() 关于
关于![]() 的任意标准正交基的矩阵都是对称矩阵;
的任意标准正交基的矩阵都是对称矩阵;
(D)![]() 关于
关于![]() 的非标准正交基的矩阵一定不是对称矩阵。
的非标准正交基的矩阵一定不是对称矩阵。
9.若![]() 是
是![]() 维欧氏空间
维欧氏空间![]() 的对称变换,则有
( )
的对称变换,则有
( )
(A)![]() 一定有
一定有![]() 个两两不等的特征根; (B)
个两两不等的特征根; (B)![]() 一定有
一定有![]() 个特征根(重根按重数算);
个特征根(重根按重数算);
(C)![]() 的特征根的个数
的特征根的个数![]() ; (D)
; (D)![]() 无特征根。
无特征根。
10.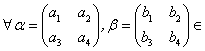
![]() ,如下定义的实数
,如下定义的实数![]() 中可做成
中可做成![]() 内积的是
( )
内积的是
( )
(A)![]() ;
(B)
;
(B)![]() ;
;
(C)![]() ; (D)
; (D)![]() .
.
四、计算题
1.把向量组![]() ,
,![]() 扩充成
扩充成![]() 中的一组正交基。
中的一组正交基。
2.已知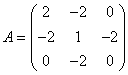 .求正交矩阵
.求正交矩阵![]() ,使
,使![]() 成对角形。
成对角形。
3.已知二次型![]() ,问
,问
(1)t为何值时二次型f是正定的?
(2)取![]() ,用正交线性替换化二次型f为标准形。
,用正交线性替换化二次型f为标准形。
4.已知二次型f(x1,x2,x3) =2x12+ax22+3x32+2bx1x2 +4x2x3 ,通过正交变换化为标准形f=y12+2y22+5y32,求a,
b及所用的正交变换的矩阵。(04xd2b)
5.设A为三阶实对称矩阵,其特征值l1= -1, l2=l3=1,已知属于l1的特征向量a1=(0,1,1)![]() ,
,
求 A.(计算04xd2b)
6.在[0,2π]上所有连续函数的全体构成的欧氏空间中,判断:对任意正整数n,集合
{cos(jx),sin(jx)|j=1,2,...,n}
是否正交向量组。
7.欧氏空间![]() 中,定义内积
中,定义内积![]() ,求其在基(1,0),(0,1)下的度量阵。并求一组基,使得在此基下的矩阵为对角阵,且在此基下所有向量的长度不变。说明为什么对角阵不是单位矩阵。
,求其在基(1,0),(0,1)下的度量阵。并求一组基,使得在此基下的矩阵为对角阵,且在此基下所有向量的长度不变。说明为什么对角阵不是单位矩阵。
8.将二次曲面![]() 通过正交变换和平移变成标准形式。
通过正交变换和平移变成标准形式。
9.设欧氏空间![]() 的线性变换
的线性变换![]() 为
为
![]()
问:![]() 是否为
是否为![]() 的对称变换?若是,求出
的对称变换?若是,求出![]() 的一个标准正交基,使
的一个标准正交基,使![]() 在这个基下的矩阵为对角形矩阵。
在这个基下的矩阵为对角形矩阵。
10.在![]() 中,镜面所在的平面方程为x+y+z=0,一个球面的方程为
中,镜面所在的平面方程为x+y+z=0,一个球面的方程为
![]()
用正交变换的方法求它在镜面上的像的方程。
五、证明题
1.设![]() ,
,![]() 为同级的正交矩阵,且
为同级的正交矩阵,且![]() ,证明:
,证明:![]() .
.
2.设![]() 是欧氏空间
是欧氏空间![]() 的线性变换,且
的线性变换,且
![]()
证明:![]() 是
是![]() 的对称变换。
的对称变换。
3.证明:![]() 维欧氏空间
维欧氏空间![]() 与
与![]() 同构的充要条件是,存在双射
同构的充要条件是,存在双射![]() ,并且
,并且![]() 有
有![]() .
.
4.设![]() 与
与![]() 为欧氏空间V的两组向量。证明:如果
为欧氏空间V的两组向量。证明:如果
![]() ,
,![]()
则子空间![]() 同构。
同构。
5.证明:在一个欧氏空间里,对于任意向量![]() ,以下等式成立:
,以下等式成立:
(1)![]() ;(2)
;(2)![]()
在解析几何里,等式(1)的几何意义是什么?
6.设![]() 为欧氏空间V的两个对称变换。证明:
为欧氏空间V的两个对称变换。证明:![]() 也是V的对称变换。
也是V的对称变换。
7.证明:实系数线性方程组![]() 有解的充分且必要条件是向量
有解的充分且必要条件是向量![]()
![]() 与齐次线性方程组
与齐次线性方程组![]() 的解空间正交。
的解空间正交。
8.设![]() 为实对称矩阵,证明:当实数t充分大后,
为实对称矩阵,证明:当实数t充分大后,![]() 是正定矩阵。
是正定矩阵。
9.设s是n维欧氏空间V的一个可逆线性变换,证明:如果V的一个子空间W在s之下不变,那么W的正交补W^在也在s之下不变。
10.设a1,a2,…,am,b1,b2,…,bm是n维欧氏空间V的两组向量,证明:存在正交变换s,使得s(ai)=bi,(i=1,2,…,m)成立的充分必要条件是<ai,aj>=<bi,bj>,i,j=1,2,…,m.
注:这里“![]() ”均表示实数域。
”均表示实数域。
编辑:忠杰
网站:瀚海网:http://hanhai.org
邮箱:nchy_zouzij@163.com
2009.5.20