第八章 矩阵习题

提高题

一．填空、计算题

1.（中国科大2008考研）矩阵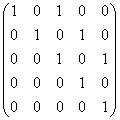的若当标准型是

2..(东南大学2004年考研)设均为n维列向量，记，求A的若当标准型。

3.（上海交大考研试题）设矩阵A=。求A的不变因子，初等因子及Jordan标准形。

4.（上海师大2005年考研）（1）设A为 3级矩阵，A与Jordan矩阵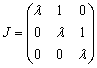相似，试介绍一种可逆矩阵的求法，使得。

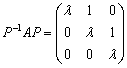（2）若，用你的方法求出矩阵P，使得。

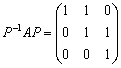5. （东南大学2002年考研）设A为 4阶矩阵，且存在正整数k，使得，又A的秩为3，分别求A与 的若尔当标准型。

6. （大连理工大学2005年考研）设3阶矩阵满足,写出的若当(Jordan)标准型的所有可能形式.

二．证明题

1. 设V为复数域上的n维线性空间，它的一个线性变换在基下的矩阵是一个若尔当块，求的所有不变子空间。

2.设为线性空间V的一个线性变换，为V的一个非零向量。证明：若每个非零的-不变子空间都包含，则存在，使得是V的一个基，且在此基下的矩阵为一个若尔当块。

编辑：忠杰

网站：瀚海网：http://hanhai.org

邮箱：nchy_zouzij@163.com

2009．5．20