第八章 λ-矩阵习题
基本题
一、填空题
1.已知5级![]() -矩阵
-矩阵![]() 的各级行列式因子:
的各级行列式因子:
![]()
则![]() 的不变因子是为_____________,
的不变因子是为_____________,![]() 的的标准形为_____________.
的的标准形为_____________.
2.设![]() 为复数域上的8阶方阵,若
为复数域上的8阶方阵,若![]() 的初等因子为:
的初等因子为:
![]()
则![]() 的为不变因子为_____________,
的为不变因子为_____________,![]() 的的若当标准形为_____________.
的的若当标准形为_____________.
3.设![]() 为复数域上的n阶方阵,若
为复数域上的n阶方阵,若![]() 的标准形为:
的标准形为:
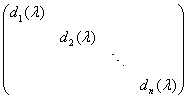
则![]() 的特征多项式
的特征多项式![]() =_____________。
=_____________。
4.矩阵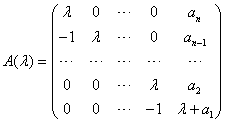 的不变因子为_____________.
的不变因子为_____________.
5.设矩阵的若当标准型为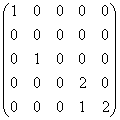 ,则此矩阵的初等因子为
.
,则此矩阵的初等因子为
.
二、判断题
1. ![]() 的
的![]() -矩阵
-矩阵![]() 可逆
可逆![]() 秩
秩![]() =n .
( )
=n .
( )
2. ![]() -矩阵
-矩阵![]() 可逆
可逆![]() ( )
( )
3. ![]() 与
与![]() 等价当且仅当它们有相同的行列式因子。
( )
等价当且仅当它们有相同的行列式因子。
( )
4. 设![]() ,则A与B相似的充要条件是它们有相同的不变因子。 ( )
,则A与B相似的充要条件是它们有相同的不变因子。 ( )
5. 复矩阵![]() 与对角矩阵相似当且仅当它的不变因子全是一次的。 ( )
与对角矩阵相似当且仅当它的不变因子全是一次的。 ( )
三.选择题
1.下列四组矩阵中,两个矩阵等价的组合为 ( )
(A) ![]() ;
(B)
;
(B) 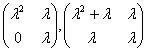 ;
;
(C)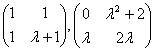 ; (D)
; (D)
![]() .
.
2.若![]() 是
是![]() 的三阶实对称矩阵的不变因子,则成立的选项是
( )
的三阶实对称矩阵的不变因子,则成立的选项是
( )
(A) ![]() 中至少有一个含一次因式的重因式;
中至少有一个含一次因式的重因式;
(B) ![]() ;
;
(C) ![]() 中都无一次因式的重因式;
中都无一次因式的重因式;
(D) ![]() .
.
3.若![]() ,则与
,则与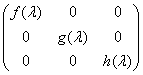 等价的阵为
( )
等价的阵为
( )
(A) 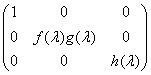 ; (B)
; (B) 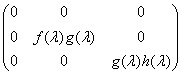 ;
;
(C) 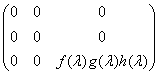 ;
(D)
;
(D) 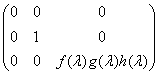 .
.
4.下列![]() 矩阵,可逆的矩阵是
( )
矩阵,可逆的矩阵是
( )
(A) 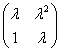 ;
(B)
;
(B) 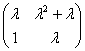 ;
;
(C) 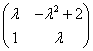 ;
(D)
;
(D) 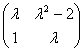 .
.
5.![]() 矩阵数字
矩阵数字![]() 的初等因子可能为
( )
的初等因子可能为
( )
(A)![]() ; (B)
; (B)
![]() ;
;
(C) ![]() ; (D)
; (D) ![]() .
.
6.设某矩阵的若尔当标准形为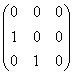 ,那么它有
( )
,那么它有
( )
(A)两个若尔当块,一个特征子空间; (B)一个若尔当块,两个特征子空间;
(C) 一个若尔当块,一个特征子空间;
(D)两个若尔当块,两个特征子空间。
四、计算题
1.设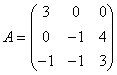
(1)求![]() 的初等因子;(2)求
的初等因子;(2)求![]() 的若当标准形。
的若当标准形。
2.化![]() -矩阵
-矩阵![]() 为标准形.
为标准形.
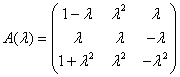
3.求矩阵 的若尔当标准形。
的若尔当标准形。
4.复数域上线性空间V的线性变换A在基![]() 下的矩阵为如下的若尔当标准型:
下的矩阵为如下的若尔当标准型:
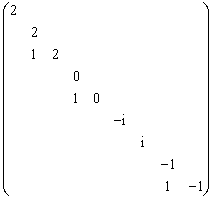
问:(1)A的值域与核的维数。
(2) 此若当标准型有几个若当块?
(3)![]() 这四个子空间中,找出不变子空间。说明理由。
这四个子空间中,找出不变子空间。说明理由。
编辑:忠杰
网站:瀚海网:http://hanhai.org
邮箱:nchy_zouzij@163.com
2009.5.20