§6 若尔当(Jordan)标准形的理论推导

现用初等因子的理论来解决若尔当标准形的计算问题.

一．若尔当标准形的初等因子.

1．若尔当块的初等因子是.

考虑它的特征矩阵

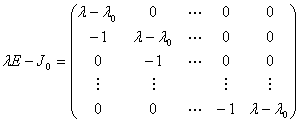
显然，这就是的n级行列式因子.由于有一个n-1级子式是                 ,

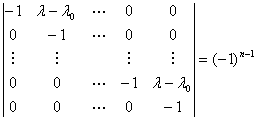所以它的n-1级行列式因子是1，从而它以下各级的行列式因子全是1.因此它的不变因子

.

由此即得，的初等因子是.

2．若尔当形矩阵的初等因子. （利用§5的定理9）

设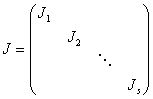是一个若尔当形矩阵，其中

.

既

然 的初等因子是 ，所以 与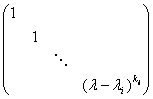

等价.于是            

与 

等价.因此，J的全部初等因子是：.

结论：(1)每个若尔当形矩阵的全部初等因子就是由它的全部若尔当块的初等因子构成的.

(2)若尔当形矩阵除去其中若尔当块排列的次序外被它的初等因子唯一决定.

由于每个若尔当块完全由它的级数n与主对角线上元素所刻划，而这两个数都反映在它的初等因子中.因此，若尔当块被它的初等因子唯一决定

二．矩阵的若尔当标准形

1．定理10 每个n级的复数矩阵A都与一个若尔当形矩阵相似，这个若尔当形矩阵除去其中若尔当块的排列次序外是被矩阵A唯一决定的，它称为A的若尔当标准形.

证明：先设出矩阵的初等因子，然后由这些初等因子构造成若当阵。由于两者有相同的初等因子，故可得它们相似。

例1 §5的例中，12级矩阵的若尔当标准形就是

例2 求矩阵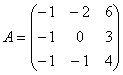 的若尔当标准形.

（先求初等因子： ，A的若尔当标准形是： ）

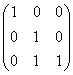注：定理10与上一章若当标准形的存在性定理（定理14），它的好处在于给出了求若当标准形的具体可操作的方法。

2．矩阵的若当标准形的求法                                               

（1）求经初等变换后的标准形

（2）通过求A的初等因子。

（3）用定理10的方法据这些初等因子构造若当标准形。（每一初等因子对应一个若当块）

3．若尔当形的存在性

定理11 设A是复数域上n维线性空间V的线性变换，在V中必定存在一组基，使A在这组基下的矩阵是若尔当形，并且这个若尔当形矩阵除去其中若尔当块的排列次序外是被A唯一决定的.

证明：由线性变换与线性变换的矩阵之间的对应关系，线性变换与线性变换的矩阵的对应关系就可以由定理10的结论推至定理11。

应该指出，若尔当形矩阵包括对角矩阵作为特殊情形，那就是由一级若尔当块构成的若尔当形矩阵，由此即得

3．复矩阵与对角阵相似的充要条件

（1）定理12 复数矩阵A与对角矩阵相似的充要条件是A的初等因子全为一次的.

   （留给同学们作练习）

（2）定理13 复数矩阵A与对角矩阵相似的充要条件是A的不变因子都没有重根.

证明：据若尔当形的作法，可以看出矩阵A的最小多项式就是A的最后一个不变因子…….

4．两点说明

1．虽然我们证明了每个复数矩阵A都与一个若尔当形矩阵相似，并且有了具体求矩阵A的若尔当标准形的方法，但是并没有谈到如何确定过渡矩阵T，使成若尔当标准形的问题. T的确定牵涉到比较复杂的计算问题.

2．如果规定上三角形矩阵

为若尔当块，应用完全类似的方法，可以证明相应于定理10，定理11的结论也成立.

     瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）