高等代数2试卷
一(30分)选择题
1.设![]() ,则下列结论
,则下列结论
不成立的是 ( )
A.![]() B.
B. ![]() 是直和
是直和
C.![]() D.
D.![]() 是直和
是直和
2.
设矩阵A=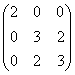 与 D=
与 D=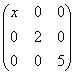 相似,则x=
( )
相似,则x=
( )
A.1
B.
3.下列不是判断线性空间的必选项的是
( )
A.加法有交换律 B. 任一向量都有长度
C. 必有零向量 D. 任一向量都有负向量
4.![]() 与
与![]() 均为线性空间
均为线性空间![]() 的子空间,则下列条件中不能断定
的子空间,则下列条件中不能断定![]() 为直和的是 ( )
为直和的是 ( )
A.![]() B.
B. ![]() 的维数=
的维数=![]() 的维数+
的维数+![]() 的维数
的维数
C. ![]() D.零向量在
D.零向量在![]() 中的表示法唯一
中的表示法唯一
5.关于若尔当标准形,下列说法正确的是 ( )
A. 若线性变换只有一个特征值,则它对应只有一个若尔当块
B. 全为一级若尔当块的若尔当标准形只有一个特征值
C.若![]() 为特征多项式的2重根,则对应有2个若尔当块
为特征多项式的2重根,则对应有2个若尔当块
D.对角形是若尔当标准形的一种
6.若在复数域中,![]() ,且
,且![]() 的首项系数均为1,则
的首项系数均为1,则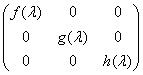 的标准形为 ( )
的标准形为 ( )
A. 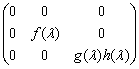 B.
B. 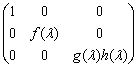
C. 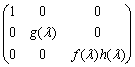 D.
D. 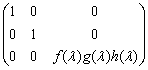
7.设![]() 都是三维向量空间
都是三维向量空间![]() 的基,且
的基,且![]() ,则矩阵
,则矩阵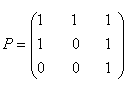 是由基
是由基![]() 到下面何组基的过渡矩阵
( )
到下面何组基的过渡矩阵
( )
![]() .
.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.![]() 是
是![]() 阶实方阵,则
阶实方阵,则![]() 是正交矩阵的充要条件是
( )
是正交矩阵的充要条件是
( )
![]() .
.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]()
9. ![]() 阶方阵
阶方阵![]() 具有
具有![]() 个不同的特征值是
个不同的特征值是![]() 与对角阵相似的
( )
与对角阵相似的
( )
![]() .充要条件;B.充分而非必要条件;C.必要而非充分条件;D.既非充分也非必要条件
.充要条件;B.充分而非必要条件;C.必要而非充分条件;D.既非充分也非必要条件
10.已知下列变换是R![]() 上的线性变换,其中是正交变换的是 ( )
上的线性变换,其中是正交变换的是 ( )
A.![]()
B.![]()
C.![]()
D.![]()
二.(12分)设3维线性空间![]() 的基为
的基为
![]()
求:1)对此基正交化成为基![]() ;2)
;2)![]() 到
到![]() 的过渡矩阵。
的过渡矩阵。
三.(14分)已知A![]() (求导函数)为线性空间R
(求导函数)为线性空间R![]() (实数域上次数小于n的多项式的全体)上的线性变换,求:1)它在基
(实数域上次数小于n的多项式的全体)上的线性变换,求:1)它在基![]() 下的矩阵。2)求上述矩阵的若尔当标准形。
下的矩阵。2)求上述矩阵的若尔当标准形。
四.(10分)设![]()
![]() ,求
,求![]() 及
及![]() 的基。
的基。
五.(10分)设![]() 是
是![]() 的子空间,求
的子空间,求![]() .
.
六.(8分)设l1, l2是线性变换A的两个不同特征值,e1, e2是分别属于l1, l2的特征向量;证明:e1+e2不是A的特征向量。
七.(8分)证明:设![]() 是向量空间V的两个子空间,那么它们的和
是向量空间V的两个子空间,那么它们的和![]() 也是
也是![]() 的一个子空间。
的一个子空间。
八.(8分)设A为m阶实对称矩阵,特征值为![]() ,B为m阶正交矩阵,证明:
,B为m阶正交矩阵,证明:![]() 为实对称阵且正定。
为实对称阵且正定。
--瀚海网原创资源--
http://hanhai.org