一.填空 (30分,每空3分)
1.Rn的子空间V={(x1,x2,…,xn) | x1+x2+…+xn=0}的维数是 。
2.A是数域P上一个n´n矩阵,f(l)=|lE-A|是A的特征多项式,则f(A)= .
3.设 s 是n维线性空间V的线性变换,则 s 的秩+ s 的零度 = .
4.已知四阶矩阵A相似于B,A的特征值为0,2,4,5,其中 E为四阶单位矩阵,则|B-E| = .
5.数域W上的所有n阶对称矩阵构成的向量空间的维数为 。
6. 设![]() 是向量空间V的一个基,线性变换s在此基下对应的矩阵为
是向量空间V的一个基,线性变换s在此基下对应的矩阵为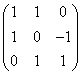 ,则s在基
,则s在基![]() 下对应的矩阵为 。
下对应的矩阵为 。
7.如果A是正交矩阵,k为实数,要使kA为正交矩阵,则k等于
。
8.数域F上任意一个n维向量空间都与 同构。
9.设V为线性空间,
A为V上的线性变换。则它的子集W成为V的A-子空间必须满足的两个条件是
和 。
二.(14分)在线性空间![]() (P为数域)中,有两组基
(P为数域)中,有两组基
![]()
与![]() .
.![]() 到
到![]() 的过渡矩阵为
的过渡矩阵为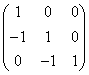 ,求基
,求基![]() 在基
在基
![]()
的坐标。并求![]() 在基
在基![]() 下的坐标。
下的坐标。
三.(12分)设矩阵A=的特征多项式有一个二重根,求a的值,并讨论A能否对角化。
四.(10分) 设 a1=(1,0,2,1), a2=(1,1,0,0), b1=(1,0,1,0), b2=(0,0,0,2).
求:(1) L(a1,a2)与L(b1,b2)的维数;
(2) L(a1,a2) + L(b1,b2)的维数;
(3) L(a1,a2)ÇL(b1,b2) 的维数.
五.(12分)在欧氏空间R3里找出单位向量h,使它们同时与向量a1=(2,2,-4), a2=(1,1,2)正交。
六.(12分)设e1,e2,e3,e4是四维线性空间V的一组基,已知线性变换 s 在这组基下的矩阵为
A = 求 s 的核与值域。
七.(12分)证明题
1.证明:如果n维线性空间V中两个子空间V1,V2的维数之和大于n,那么V1,V2含有非零的公共向量。
2.设![]() 是线性空间V的一个线性变换,且
是线性空间V的一个线性变换,且![]() (k>0),求证
(k>0),求证![]() 线性无关。
线性无关。