高等代数2试卷2A      答案   返回

 

一、填空（每空3分,共33分）

 

1.设V为线性空间,为V中线性无关的向量组,则V的子空间的维数为        .

2．设矩阵的若当标准型为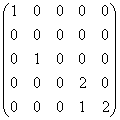，则此矩阵的初等因子为           .其不变因子为        .若它是某线性空间的线性变换在某组基下的矩阵,则它对应有   个线性无关的特征向量。

3.若n维线性空间V中的线性变换的秩为r ,那么的核的维数为      .

4. 设三阶方阵A的三个特征值为1，2，-2，则=      .

5.设实二次型，其中二次型的矩阵的特征值之和为1，特征值之积为.则      ,       .

6.若欧氏空间在某组基下的度量矩阵为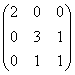,某向量在此组基下的坐标为,则它的长度为       。在此基下,向量与向量 的夹角为       .

7.同构的线性空间的维数       .

 

二、（15分）设维线性空间R4的两组基分别为

    

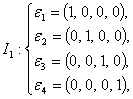
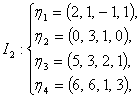
求：（1）由基到基的过渡矩阵；（2）在基下的坐标；（3）在基和基下有相同坐标的全体向量。

 

 

 

 

 

 

 

 

 

 

 

 

 

三、（15分）设实数域上线性空间的线性变换在某组基下的

矩阵为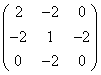.求它在正交变换下的标准形(要求写出正交变换)。

 

 

 

 

 

 

               

 

                

 

 

 

 

 

 

 

四.(15分)设已知线性空间V=(数域P上的二阶方阵全体.加法定义为矩阵的加法;数乘为矩阵的数乘)。

                   

判断:(1)V1是否为V的子空间?它的基与维数?

(2)若在V中定义变换:

              

            

A是否为V上的线性变换?

(3)V1是否为-子空间,说明理由。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

五(12分)设是数域上线性空间的线性变换且,证 明:

1)的核；

2) 的特征值为0或1.

 

 

 

 

 

 

 

 

 

 

 

六、（10分）设是欧氏空间的一组基，证明：（1）如果使，则；（2）如果使对任意有 ，则.

　

　

　

　

　

                                                  

                                                                                                  --瀚海网原创资源--

                                                                                                     http://hanhai.org